Longest Bitonic Subsequence

Difficulty Level Hard
Frequently asked in CodeNation DE Shaw Google JP Morgan Microsoft
Array Dynamic ProgrammingViews 2128

Suppose you have an array of integers, the problem statement asks to find out the longest bitonic subsequence. The bitonic sequence of an array is considered as the sequence which first increases and then decreases.

Example

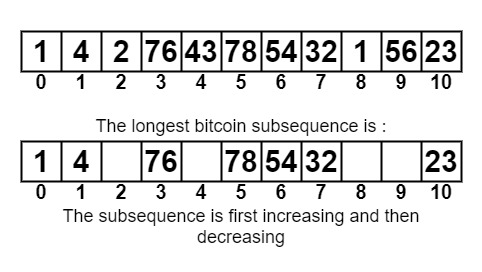
arr[] = {1,4,2,76,43,78,54,32,1,56,23}
7

Explanation

1 ⇒ 4 ⇒ 76 ⇒ 78 ⇒ 54 ⇒ 32 ⇒ 23 (First Increasing up to 78 and then decreasing till 23.

Longest Bitonic Subsequence

 

Algorithm

  1. Declare an array increasingSeq[] of size same as the length of the given array length.
  2. Initialize all the indices elements as 1 of created array increasingSeq[].
  3. Find out the longest increasing subsequence by storing it in the increasingSeq[] from left to right.
  4. Declare an array decreasingSeq[] of size same as the length of the given array.
  5. Find the longest decreasing subsequence traversing from right to left and by storing it into the decreasingSeq[].
  6. Initialize a variable called maxOutput to increasingSeq[0] + decreasingSeq[0] – 1.
  7. Find out the maximum of increasingSeq[i] + decreasingSeq[i] – 1 and store it to maxOutput.
  8. Return the maxOutput.

Explanation

The input array of size n consists of positive integers. We are asked to find out the longest bitonic sequence of the given array. The bitonic sequence can be defined as the sequence which increases first, which means the number in the sequence first increases. Then the number decreases until the end of the sequence. We need to determine the length of the longest bitonic sequence.

First, separate the solution in two-parts. We declare two arrays, the first array is considered as an increasingSeq array. The longest increasing sequence is the sequence in which the numbers should be first in an increasing sequence. So, we are going to traverse the array in a nested loop. Keep on finding increasing subsequence. Then we have to check a condition that if the current element is less than the next element. And also the increasingSeq’s current element is less than the next element of increasingSeq[]. If true then store the element as increasingSeq[j] + 1. This adds up because we have already initialized the array as 1 in it.

Second, declare an array, decreasingSeq[]. In this decreasingSeq[], we are going to traverse the array in a nested loop fashion, from right to left of the array. We are going to check if the current element is greater than the next element. Because we are traversing from right to left. Then update it to the decreasingSeq[i] to the decreasingSeq[j]+1. In the last step of the code, we need to find the maximum of increasingSeq[i] + decreasingSeq[i] – 1 which is stored in maxOutput.

Code

C++ code for Longest Bitonic Subsequence

#include<iostream>

using namespace std;

int BitonicSequence( int arr[], int n )
{
    int i, j;

    int *increasingSeq = new int[n];
    for (i = 0; i < n; i++)
        increasingSeq[i] = 1;

    for (i = 1; i < n; i++)
        for (j = 0; j < i; j++)
            if (arr[i] > arr[j] && increasingSeq[i] < increasingSeq[j] + 1)
                increasingSeq[i] = increasingSeq[j] + 1;

    int *decreasingSeq = new int [n];
    for (i = 0; i < n; i++)
        decreasingSeq[i] = 1;

    for (i = n-2; i >= 0; i--)
        for (j = n-1; j > i; j--)
            if (arr[i] > arr[j] && decreasingSeq[i] < decreasingSeq[j] + 1)
                decreasingSeq[i] = decreasingSeq[j] + 1;

    int maxOutput = increasingSeq[0] + decreasingSeq[0] - 1;

    for (i = 1; i < n; i++)
        if (increasingSeq[i] + decreasingSeq[i] - 1 > maxOutput)
            maxOutput = increasingSeq[i] + decreasingSeq[i] - 1;

    return maxOutput;

}
int main()
{
    int arr[] = {1,4,2,76,43,78,54,32,1,56,23};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout<<"Length of Longest Bitonic Sequence is "<< BitonicSequence(arr, n);
    return 0;
}

Length of Longest Bitonic Sequence is 7

Java code for Longest Bitonic Subsequence

class longestBitonicSequence
{
    public static int BitonicSequence( int arr[], int n )
    {
        int i, j;

        int[] increasingSeq = new int[n];
        for (i = 0; i < n; i++)
            increasingSeq[i] = 1;

        for (i = 1; i < n; i++)
            for (j = 0; j < i; j++)
                if (arr[i] > arr[j] && increasingSeq[i] < increasingSeq[j] + 1)
                    increasingSeq[i] = increasingSeq[j] + 1;

        int[] decreasingSeq = new int [n];
        for (i = 0; i < n; i++)
            decreasingSeq[i] = 1;

        for (i = n-2; i >= 0; i--)
            for (j = n-1; j > i; j--)
                if (arr[i] > arr[j] && decreasingSeq[i] < decreasingSeq[j] + 1)
                    decreasingSeq[i] = decreasingSeq[j] + 1;


        int maxOutput = increasingSeq[0] + decreasingSeq[0] - 1;

        for (i = 1; i < n; i++)
            if (increasingSeq[i] + decreasingSeq[i] - 1 > maxOutput)
                maxOutput = increasingSeq[i] + decreasingSeq[i] - 1;

        return maxOutput;
    }

    public static void main (String[] args)
    {
        int arr[] = {1,4,2,76,43,78,54,32,1,56,23};
        int n = arr.length;
        System.out.println("Length of longest bitonic sequence is "+ BitonicSequence( arr, n ));
    }
}

Length of longest bitonic sequence is 7

Complexity Analysis

Time Complexity

O(n2) where “n” is the number of elements in the array. Since we used a nested loop which made the algorithm run in polynomial time.

Space Complexity

O(n) where “n” is the number of elements in the array. Since we used two extra arrays whose size is dependent on the input array. The space complexity is linear.

Translate »