Print n terms of Newman-Conway Sequence

Problem Statement

The problem “Print n terms of Newman-Conway Sequence” states that you are given an integer “n”. Find the first n terms of Newman-Conway Sequence then print them.

Example

n = 6

1 1 2 2 3 4

Explanation
All the terms which are printed follow the Newman-Conway Sequence and thus we need to do the same. We will try to find the first n terms.

Approach to print n terms of Newman-Conway Sequence

The Newman-Conway Sequence is a sequence whose each term satisfies the following recurrence relation:

P(1) = P(2) = 1

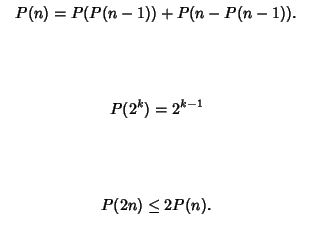
Now what we need to do is find the first n terms of the sequence. We have already solved a similar problem where we had to find the nth element of the Newman-Conway Sequence. At that time, we had two options. Either we could solve the problem using recursion or we could have used Dynamic Programming. We learned that using recursion will exceed the time limit. Since the time complexity of Recursion is exponential. For the recursion solution, we will use the recurrence formula and will keep on calculating the values for different elements. Consider you need to find P(3), so you will find P(P(2)) and P(3-P(2)). So to find P(3), first, you need to calculate P(2), then again do the same calculations. This task is very time-consuming.

Dynamic Programming Approach

So as to reduce time complexity, we used dynamic programming. Because we were calculating some of the elements multiple times. Instead of calculating the elements multiple times, we stored the answer for intermediate elements. The technique is very similar to recursion. But there is the addition of a single part which is using a memoization table. The memoization stores the values for each calculated term.

So whenever we need some term, we simply just check if it is already calculated. If not we compute it, else use it. This technique of storing intermediate terms is generally known as Dynamic Programming. Thus we will keep on caching the values and at last, we will print these values.

Code

C++ code to Print n terms of Newman-Conway Sequence

#include <bits/stdc++.h>
using namespace std;
int main(){
  // elements to be printed
  int n;cin>>n;
  int dp[n+1];
  dp[0] = 0;
  dp[1] = dp[2] = 1;
  for(int i=3;i<=n;i++)
    dp[i] = dp[dp[i-1]] + dp[i-dp[i-1]];
  for(int i=1;i<=n;i++)
  	cout<<dp[i]<<" ";
}

6

1 1 2 2 3 4

Java code to Print n terms of Newman-Conway Sequence

import java.util.*;
class Main{
    public static void main(String[] args){
      Scanner sc = new Scanner(System.in);
    // elemnts to be printed
    int n = sc.nextInt();
    int dp[] = new int[n+1];
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 1;
    for(int i=3;i<=n;i++)
      dp[i] = dp[dp[i-1]] + dp[i-dp[i-1]];
  	for(int i=1;i<=n;i++)
    	System.out.print(dp[i]+" ");
  }
}

6

1 1 2 2 3 4

Complexity Analysis

Time Complexity

O(N), because we just ran a loop in a dynamic programming approach. As we always had all the elements recalculated which were required for the computation of the current element.

Space Complexity

O(N), storing all n elements requires linear space and thus the space complexity is also linear.