Print the Fibonacci numbers in reverse order

Difficulty Level Easy
Frequently asked in Accenture MAQ o9 solutions UHG Optum
Dynamic Programming SequenceViews 9224

Problem Statement

Given a number n, print the fibonacci numbers in reverse order.

Example

n = 5
3 2 1 1 0

Explanation: The Fibonacci numbers are 0, 1, 1, 2, 3 as per their ordering. But since we needed to print in reverse order.

n = 7
8 5 3 2 1 1 0

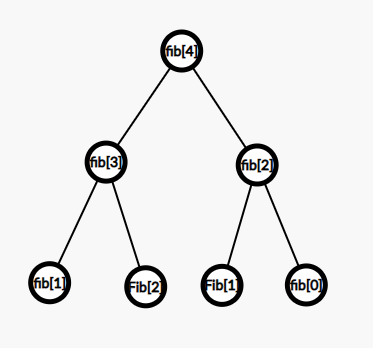
Print the Fibonacci numbers in reverse order

The figure denotes how Fibonacci numbers are dependent on the result of the last 2 Fibonacci numbers.

Algorithm

  1. Take input, the number of elements to be printed.
  2. Declare an array of size as that of the given input.
  3. Initialize the 0th and 1th array index with 0 and 1.
  4. We start to run a loop from i = 2, until the value of i is less than n while incrementing the value of i one by one.
    1. Keep storing the addition of the last index element and last to last index element.
  5. Now print this array in reverse order.

Approach

A naive approach to print Fibonacci numbers has always been recursion. And whenever we are told about recursion, the first thing we generally are told about are Fibonacci numbers. So, using recursion we can find the Fibonacci numbers. And then simply print them in reverse order. But doing this requires heavy computation, so instead of doing that we need to think of an alternative approach.

The alternative approach is dynamic programming, where we store the data which is required more often in solving the problem. We have also discussed finding fibonacci numbers using dynamic programming in the previous post.

Code

C++ code to print fibonacci numbers in reverse order

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n;cin>>n;
    int fib[n];
    if(n>=1)
    fib[0] = 0;
    if(n>=2)
    fib[1] = 1;
    for(int i=2;i<n;i++)
        fib[i] = fib[i-1] + fib[i-2];
    for(int i=n-1;i>=0;i--)
        cout<<fib[i]<<" ";
}

4
2 1 1 0

Java code to print fibonacci numbers in reverse order

import java.util.*;
class Main{
  
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    	int fib[] = new int[n];
    	if(n>=0)
    		fib[0] = 0;
    	if(n>=1)
    		fib[1] = 1;
    	for(int i=2;i<n;i++)
    		fib[i] = fib[i-1] + fib[i-2];
    	for(int i=n-1;i>=0;i--)
    		System.out.print(fib[i]+" ");
  	}
}
4
2 1 1 0

Complexity Analysis

Time Complexity

O(N), this time is required to compute the fibonacci numbers. Because we just run a single loop to find the fibonacci sequence. The time complexity is linear.

Space Complexity

O(N), because we have used an array to store the values of fibonacci numbers, the space complexity is linear.

Translate »