Table of Contents
Problem Statement
The “Queries for GCD of all numbers of an array except elements in a given range” problem states that you will be given an integer array and a q number of queries. Each query contains the number left and right. The problem statement asks to find out the greatest common divisor of all the integers except within the given range of the query.
Example
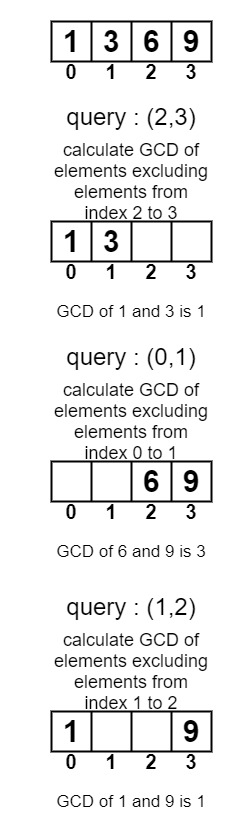
arr[] = {1, 3, 6, 9}
Query: {(2, 3), (0, 1), (1, 2)}1 3 1
Explanation
The GCD of elements excluding elements from index 2 to 3 i.e., GCD of 1 and 3 is 1
Now the GCD of elements excluding elements from index 0 to 1 i.e., GCD of 6 and 9 is 3
Again the GCD of elements excluding elements from index 1 to 2 i.e., GCD of 1 and 9 is 1
Algorithm
- Create two arrays of size as same as that of the given input array.
- Traverse the array from 1 index to the length of the array. Then find out the GCD of the current element and element stored at previous index in preArray and store it at current index in preArray.
- Traverse the array from the right to left, and find out the GCD of the suffixArray element and the given array element and store the GCD into the suffixArray.
- For each given query, if the left range is equal to 0, then return the value of suffixArray[right+1].
- Else if the value of right is equal to n – 1, then return the value of preArray[left – 1].
- Else return the value of the GCD of the preArray[left-1] and the suffixArray[right+1].
Explanation
Given an array of integers and queries to answer. We are asked to find out the greatest common divisor of the numbers except for all the integers in the given range of the query. If we are given a range of 0 to 1 in an array of length 5. This means we have to find out the greatest common divisor of all the integers except arr[0] and arr[1] in an array. Given query which contains the left and right as a range. We have to leave the integers that come in this range.
We are going to traverse the array but before that copy the first element of the given array into the preArray’s first element. After that traverse the array from left to right. During this time we will be building the preArray and suffixArray. For preArray find out the Greatest Common Divisor of element at current index in original input array and element at previous index in preArray. Store this GCD of these numbers in the preArray element. After the traversal of the array, build the suffixArray. For that, at the place of the last element of the suffixArray. Copy the last element of the array of the given array element. After that follow the same procedure as we follow for the preArray but from right to left of the array.
For each given query of the given range, check if the given left range is equal to 0. Thus return the value of suffixArray[right+1]. Check if the value of right is equal to the length of the array. Then return the value of preArray[left -1]. Else return the greatest common divisor of the element at left index in preArray and element at right index in suffixArray. That will be our required answer.
Code
C++ code for finding GCD of array except a given range
#include<iostream>
using namespace std;
int __GCD(int a, int b)
{
if (b == 0)
return a;
return __GCD(b, a % b);
}
void buildArrayOfGCD(int PreArray[], int arr[], int suffixArray[], int n)
{
PreArray[0] = arr[0];
for (int i=1 ; i<n; i++)
PreArray[i] = __GCD(PreArray[i-1], arr[i]);
suffixArray[n-1] = arr[n-1];
for (int i=n-2; i>=0 ; i--)
suffixArray[i] = __GCD(suffixArray[i+1], arr[i]);
}
int getGCDInRange(int l, int r, int PreArray[], int suffixArray[], int n)
{
if (l==0)
return suffixArray[r+1];
if (r==n-1)
return PreArray[l-1];
return __GCD(PreArray[l-1], suffixArray[r+1]);
}
int main()
{
int arr[] = {1, 3, 6, 9};
int n = sizeof(arr)/sizeof(arr[0]);
int PreArray[n], suffixArray[n];
buildArrayOfGCD(PreArray, arr, suffixArray, n);
int l = 2, r = 3;
cout << getGCDInRange(l, r, PreArray, suffixArray, n)
<< endl;
l = 0 ;
r = 1;
cout << getGCDInRange(l, r, PreArray, suffixArray, n)
<< endl;
l = 1 ;
r = 2;
cout << getGCDInRange(l, r, PreArray, suffixArray, n)
<< endl;
return 0;
}
1 3 1
Java code for finding GCD of array except a given range
import java.util.*;
class GCDNumbers
{
static int GCD(int a, int b)
{
if (b == 0)
return a;
return GCD(b, a % b);
}
static void buildArrayOfGCD(int preArray[],int arr[], int suffixArray[], int n)
{
preArray[0] = arr[0];
for (int i = 1; i < n; i++)
preArray[i] = GCD(preArray[i - 1], arr[i]);
suffixArray[n - 1] = arr[n - 1];
for (int i = n - 2; i >= 0; i--)
suffixArray[i] = GCD(suffixArray[i + 1], arr[i]);
}
static int getGCDInRange(int l, int r, int preArray[], int suffixArray[], int n)
{
if (l == 0)
return suffixArray[r + 1];
if (r == n - 1)
return preArray[l - 1];
return GCD(preArray[l - 1], suffixArray[r + 1]);
}
public static void main(String[] args)
{
int arr[] = { 1, 3, 6, 9};
int n = arr.length;
int preArray[] = new int[n];
int suffixArray[] = new int[n];
buildArrayOfGCD(preArray, arr, suffixArray, n);
int l = 2, r = 3;
System.out.println(getGCDInRange(l, r, preArray, suffixArray, n));
l = 0;
r = 1;
System.out.println(getGCDInRange
(l, r, preArray, suffixArray, n));
l = 1;
r = 2;
System.out.println(getGCDInRange
(l, r, preArray, suffixArray, n));
}
}
1 3 1
Complexity Analysis
Time Complexity
O(N+Qlogn) where “Q” is the number of queries and “N” is the number of elements in the input array. O(N) time is required to required for the building of the preArray and suffixArray. Then O(Qlog n) time is required to answer the queries because for answer each query we are finding gcd of two numbers which costs us log n where n is the number and log is with base 2.
Space Complexity
The space complexity for solving Queries for GCD of all numbers of an array except elements in a given range is O(N) where “N” is the number of elements in the array for storing the preArray and suffixArray.