Range Queries for Longest Correct Bracket Subsequence

You are given a sequence of some brackets subsequence, in other words, you are given brackets like ‘(’ and ‘)’ and you are given a query range as a starting point and ending point. The problem “Range Queries for Longest Correct Bracket Subsequence” asks to find out the maximum length of correct bracket subsequence or balanced parenthesis brackets, within a given query range, like “()()”, “(())”, “((()))” etc.

Table of Contents

Example

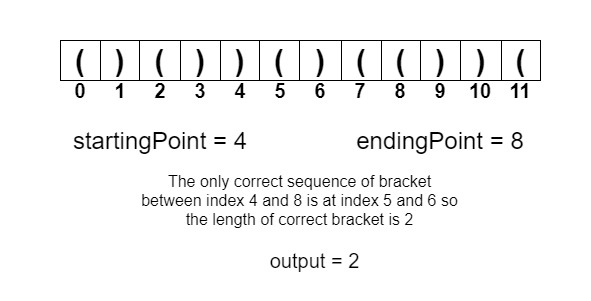
String s = “()())()(())( ”
startingPoint = 4
endingPoint = 8

Explanation

The only correct brackets are at index 5 and 6.

Range Queries for Longest Correct Bracket Subsequence

Algorithm

Declare a Stack.
Traverse the complete string and push all the opening brackets into the stack.
1. If it is not opening bracket then check if the stack is not empty, then mark that index as 1.
  1. Get the size of the stack and mark that index to 1, and pop the top element from stack.
2. If the stack is empty then mark that index having closed bracket as 0.
Traverse till the length of the string and sum up each of the element as following.
1. closedBrackets[i] = closedBrackets[i] + closedBrackets[i-1]
2. openingBrackets[i] = openingBrackets[i] + openingBrackets[i-1]
Take the query as startingPoint and endingPoint.
1. Check if openingBrackets[startingPoint-1]= openingBrackets[startingPoint]
  1. Return ( closedBrackets[ endingPoint ] – openingBrackets[ startingPoint ]) * 2.
2. Else return (closedBrackets[ endingPoint ]- openingBrackets[ startingPoint ] + 1) * 2.

Explanation

We are given a string of sequence of brackets, in which ‘(’ and ‘)’ type of parenthesis are present, and a range of queries are given. Queries are given in the form of a starting point and an ending point of the subarray. We are asked to find out the maximum length of correct or balanced parenthesis, within the given range. Correct or balanced brackets can be considered as equal no of opening or closing brackets. But we are given a range, we have to find the maximum length that is possible with a correct subsequence of brackets.

In order to find out, Stack like data structure will be beneficial. We are going to push all the opening brackets into the stack so that we can find from where we have to start. If the current bracket is not an opening bracket. We have to check if the stack should not be empty for doing further operations. Of course, it will be a closing bracket. If it is not an opening bracket, then we mark that closing bracket index as 1. And in the next step, we will get the size of the stack and treat that size as an index and mark that index as 1 of openingBrackets, and pop the element of the stack. Traverse till the length of the string, and sum up each value of the openingBrackets and closingBrackets and store the sum at each index.

Take the queries as input, and check in the closingBrackets if the starting point value is equal to the previous value of openingBrackets then return the number as twice of the difference of closingBrackets[endingPoint] – openingBrackets[startingPoint]. Else return the number as twice of difference of closingBrackets[endingPoint] – openingBrackets[startingPoint] + 1. We will get the desired answer.

Code

C++ code to answer range queries for Longest Correct Bracket Subsequence

#include<iostream>
#include<cstring>
#include<stack>

using namespace std;

void correctBracketsLength(int OPENINGBRACKETS[], int CLOSEDBRACKETS[], char* str, int n)
{
    stack<int> STACK;
    int result = 0;
    for (int i = 0; i < n; i++)
    {
        if (str[i] == '(')
            STACK.push(i);
        else
        {
            if (!STACK.empty())
            {
                CLOSEDBRACKETS[i] = 1;
                OPENINGBRACKETS[STACK.top()] = 1;
                STACK.pop();
            }
            else
                CLOSEDBRACKETS[i] = 0;
        }
    }
    for (int i = 1; i < n; i++)
    {
        CLOSEDBRACKETS[i] += CLOSEDBRACKETS[i - 1];
        OPENINGBRACKETS[i] += OPENINGBRACKETS[i - 1];
    }
}
int query(int OPENINGBRACKETS[], int CLOSEDBRACKETS[], int startingPoint, int endingPoint)
{
    if (OPENINGBRACKETS[startingPoint - 1] == OPENINGBRACKETS[startingPoint])
    {
        return (CLOSEDBRACKETS[endingPoint] - OPENINGBRACKETS[startingPoint]) * 2;
    }
    else
    {
        return (CLOSEDBRACKETS[endingPoint] - OPENINGBRACKETS[startingPoint] + 1) * 2;
    }
}
int main()
{
    char str[] = "()())()(())(";
    int n = strlen(str);

    int CLOSEDBRACKETS[n + 1] = { 0 };
    int OPENINGBRACKETS[n + 1] = { 0 };

    correctBracketsLength(OPENINGBRACKETS, CLOSEDBRACKETS, str, n);

    int startingPoint = 4, endingPoint = 8;

    cout << "Maximum Length within "
         << startingPoint << " and " << endingPoint << " = "
         << query(OPENINGBRACKETS, CLOSEDBRACKETS, startingPoint, endingPoint) << endl;

    return 0;
}

Maximum Length within 4 and 8 = 2

Java code to answer range queries for Longest Correct Bracket Subsequence

import java.util.*;

class LongestCorrectBracket
{
    public static void correctBracketsLength(int OPENINGBRACKETS[], int CLOSEDBRACKETS[], String str, int n)
    {
        Stack<Integer> STACK = new Stack<>();;

        for(int i = 0; i < n; i++)
        {
            if (str.charAt(i) == '(')
                STACK.add(i);
            else
            {
                if (!STACK.isEmpty())
                {
                    CLOSEDBRACKETS[i] = 1;
                    OPENINGBRACKETS[STACK.peek()] = 1;
                    STACK.pop();
                }
                else
                    CLOSEDBRACKETS[i] = 0;
            }
        }
        for(int i = 1; i < n; i++)
        {
            CLOSEDBRACKETS[i] += CLOSEDBRACKETS[i - 1];
            OPENINGBRACKETS[i] += OPENINGBRACKETS[i - 1];
        }
    }
    static int query(int OPENINGBRACKETS[], int CLOSEDBRACKETS[], int startingPoint, int endingPoint)
    {
        if (OPENINGBRACKETS[startingPoint - 1] == OPENINGBRACKETS[startingPoint])
        {
            return (CLOSEDBRACKETS[endingPoint] - OPENINGBRACKETS[startingPoint]) * 2;
        }
        else
        {
            return (CLOSEDBRACKETS[endingPoint] - OPENINGBRACKETS[startingPoint] + 1) * 2;
        }
    }
    public static void main(String[] args)
    {
        String str = "()())()(())(";
        int n = str.length();

        int CLOSEDBRACKETS[] = new int[n + 1];
        int OPENINGBRACKETS[] = new int[n + 1];

        correctBracketsLength(OPENINGBRACKETS, CLOSEDBRACKETS, str, n);

        int startingPoint = 4, endingPoint = 8;
        System.out.print("Maximum Length within " +
                         startingPoint + " and " + endingPoint +
                         " = " + query(OPENINGBRACKETS, CLOSEDBRACKETS, startingPoint,
                                       endingPoint) + "\n");
    }
}

Maximum Length within 4 and 8 = 2

Complexity Analysis

Time Complexity

O(1) for each query performed. But the precomputation requires O(n+q) time. Thus the total time complexity of the algorithm is linear.

Space Complexity

O(n) where “n” is the length of the string. Since we created two arrays for storing the opening bracket and closing bracket count. The space complexity is linear.