Count subarrays having total distinct elements same as original array

Table of Contents

Problem Statement

“Count subarrays having total distinct elements same as original array” states that you are given an integer array. The problem statement asks to find out the total number of sub-arrays that contain all distinct elements as present in an original array.

Example

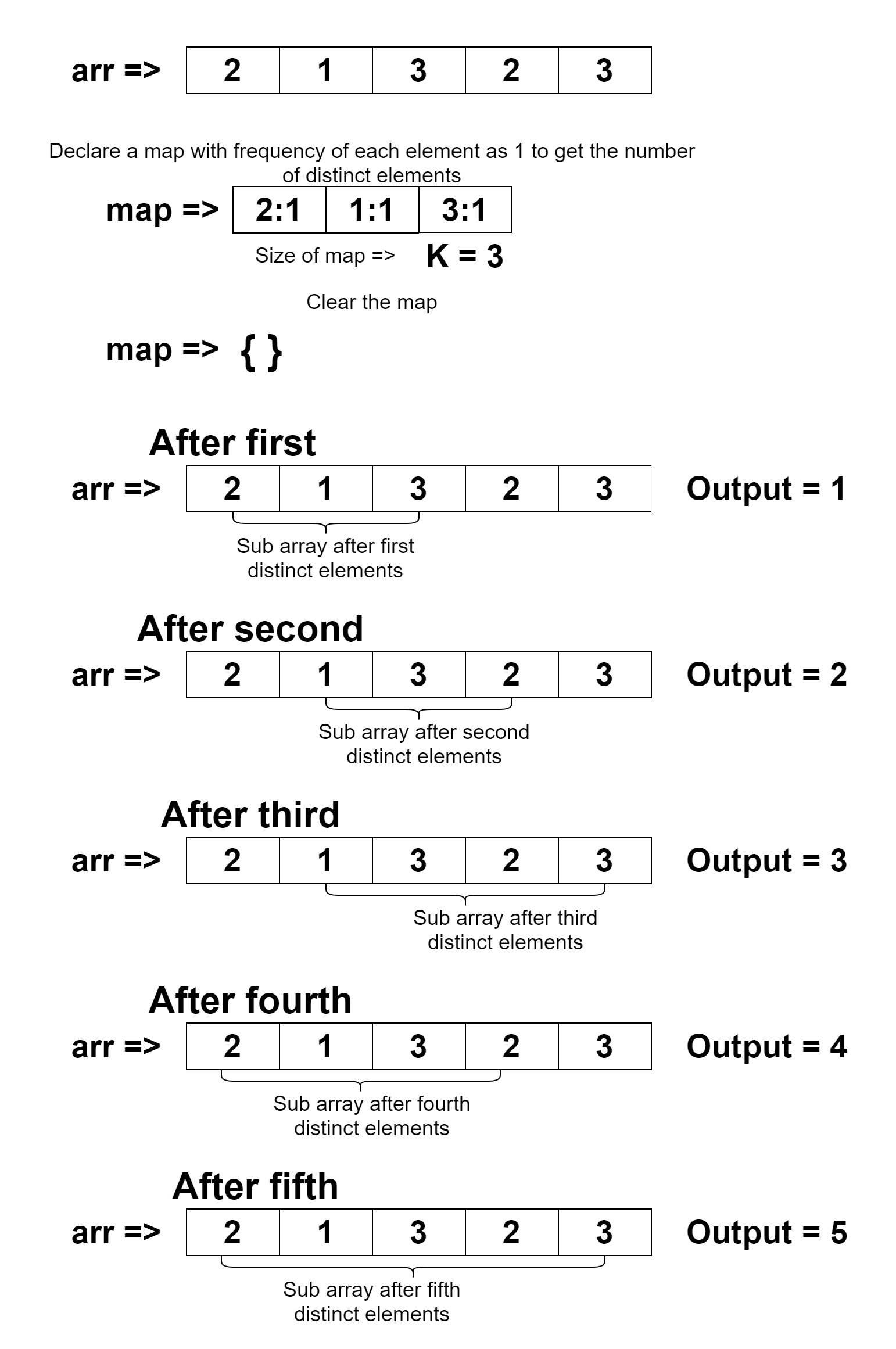
arr[] = {2, 1, 3, 2, 3}

Explanation: Sub-array ⇒ {2, 1, 3}, {1, 3, 2}, {1, 3, 2, 3}, {2, 1, 3, 2} and {2, 1, 3, 2, 3} contain all distinct elements as original array.

Count subarrays having total distinct elements same as original array

arr[] = {2, 4, 3, 4, 1, 2}

Explanation: Sub-array ⇒ {3, 4, 1, 2}, {4, 3, 4, 1, 2}, {2, 4, 3, 4, 1} and {2, 4, 3, 4, 1, 2} contain all distinct elements as original array.

Algorithm to Count subarrays having total distinct elements same as original array

1. Declare a map.
2. Add all the values of array into the map with 1 as each key’s value.
3. Find the size of the map, store it to k and clear the map.
4, Set output, right, and maxsa to 0.
5. Traverse the array, from i=0, to i < n(length of the array).
  1. While the right is less than n and maxsa is less than k,
    1. Insert arr[right] and increase its frequency by 1.
    2. Check if the map’s value of current array element (arr[right]) is equal to 1 if true then increase the count of maxsa by 1.
  2. Increase the count of right by 1.
  3. If maxsa is equal to k, then update output à output += (n - right + 1).
  4. Insert the value of current arr[left] and decrease its frequency by 1.
  5. If the map’s arr[left] is equal to 0, then decrease the value of maxsa by 1.
6. Return output.

Explanation

We have given an integer array, we are asked to find out the total number of sub-arrays that contain all distinct elements as present in an original array. For this, we will use Hashing. It is an efficient approach to solve this code.

Declare a map. We are going to traverse the whole array, and put each element into the map with only a frequency that is 1. Because we do not want to count the frequency of each element. This is just to know how many unique keys are present in a given array. We will store the size of the map into the variable k and clear the map.

We are going to traverse the whole array. But before that, we set the value of output, right and maxsa to 0. Starting from 0, we will enter again in a loop in search of a sub-array, while the right is less than n and maxsa is less than k. Now, we will put the array element and increase its frequency by 1. We will check if the current element has a frequency of 1. Or we just updated it to more of that, if it is found to be true, then increase the value of maxsa.

After coming out of the while loop, you will have an incremented value of maxsa, if it is equal to k, then update the output to n-right +1. As we already put the values of array element into the map. Now we will decrease its frequency by 1, and check if arr[left] value is equal to 0 and decrease the maxsa value. Whenever we found the value of maxsa to k we will update the output value.

Code

C++ code to count subarrays having total distinct elements same as original array

#include<iostream>
#include<unordered_map>

using namespace std;

int getSubArrayDistinct(int arr[], int n)
{
    unordered_map<int, int> MAP;
    for (int i = 0; i < n; ++i)
        MAP[arr[i]] = 1;

    int k = MAP.size();

    MAP.clear();

    int output = 0, right = 0, maxsa = 0;
    for (int left = 0; left < n; ++left)
    {
        while (right < n && maxsa < k)
        {
            ++MAP[ arr[right] ];

            if (MAP[ arr[right] ] == 1)
                ++maxsa;

            ++right;
        }
        if (maxsa == k)
        {
            output += (n - right + 1);
        }
        --MAP[ arr[left] ];

        if (MAP[ arr[left] ] == 0)
        {
            --maxsa;
        }
    }
    return output;
}
int main()
{
    int arr[] = {2, 1, 3, 2, 3};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << getSubArrayDistinct(arr, n);
}

Java code to Count subarrays having total distinct elements same as original array

import java.util.HashMap;

class SubarrayWithDistinctEle
{
    public static int getSubArrayDistinct(int arr[], int n)
    {
        HashMap<Integer, Integer> MAP = new HashMap<Integer,Integer>()
        {
            @Override
            public Integer get(Object key)
            {
                if(!containsKey(key))
                    return 0;
                return super.get(key);
            }
        };

        for (int i = 0; i < n; ++i)
            MAP.put(arr[i], 1);
        int k = MAP.size();

        MAP.clear();

        int output = 0, right = 0, maxsa = 0;
        for (int left = 0; left < n; ++left)
        {
            while (right < n && maxsa < k)
            {
                MAP.put(arr[right], MAP.get(arr[right]) + 1);

                if (MAP.get(arr[right])== 1)
                {
                    ++maxsa;
                }

                ++right;
            }
            if (maxsa == k)
            {
                output += (n - right + 1);
            }

            MAP.put(arr[left], MAP.get(arr[left]) - 1);

            if (MAP.get(arr[left]) == 0)
                --maxsa;
        }
        return output;
    }
    public static void main(String args[])
    {
        int arr[] = {2, 1, 3, 2, 3};
        int n=arr.length;
        System.out.println(getSubArrayDistinct(arr, n));
    }
}

Complexity Analysis

Time Complexity

O(N) where “N” is the number of elements in the array. Since we have traversed the array and have used HashMap which made us achieve linear time complexity.

Space Complexity

O(N) where “N” is the number of elements in the array. Because we have used an array to store the input and a HashMap which is going to store N elements. Thus linear space complexity is achieved.