Table of Contents
Problem Statment
Cuckoo sequence program or Cuckoo Hashing is a method used to solve the problem when a collision occurs in a Hash Table. Collisions are likely of two hash values of a hash function in a table. A collision occurs when two hash values for the same key occurs in the hash function of a table. To resolve that collision we use Cuckoo Hashing.
As from the name, Cuckoo Hashing is just derived from some characteristic of a cuckoo, as a chick of the cuckoo shove or pushes the other eggs or the young ones out of the nest to make a place for own. The same we do in Cuckoo Hashing, trying to insert a new key into the hash table we just push the older key to the new place. And that is how Cuckoo Hashing implemented.
Collision
When a new key, which we try to insert in a Hash Table find an already occupied place in a Hash Table. In that case, this situation is called a collision. When a new key indicates a place to be inserted which is already occupied in a Hash Table is called a collision.
This situation can be handled by using some of the Collision handling techniques.
- Closed Addressing or Separate Chaining
- Open Addressing
Closed Addressing or Separate Chaining
The Separated Chaining is one of the techniques to handle collision problems of Hash Tables. In Separate Chaining, the concept is to join a cell to a linked list to store records for the same hash function values.
Open Addressing
Open Addressing is also a method to resolve the problem of collision. In Open Addressing, all of the keys and values are stored in a Hash Table. The size of the table should be greater than or equal to the keys present in a Hash Table, and it can occur at any point.
Cuckoo Hashing
In a Cuckoo Hashing, there are two concepts that this method used to achieve the implementation which has guaranteed O(1) worst-case Look-Up time.
Those concepts are:
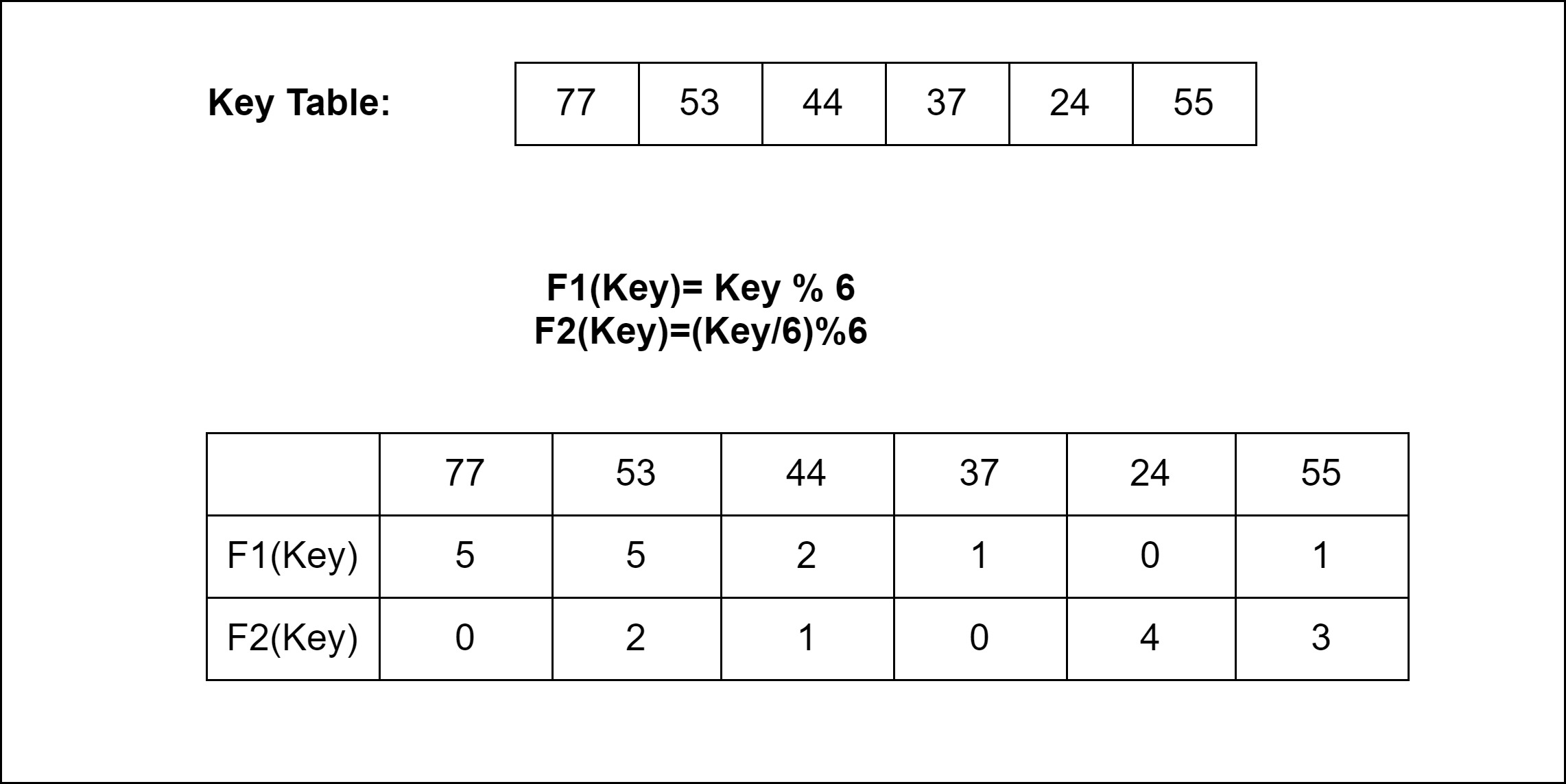
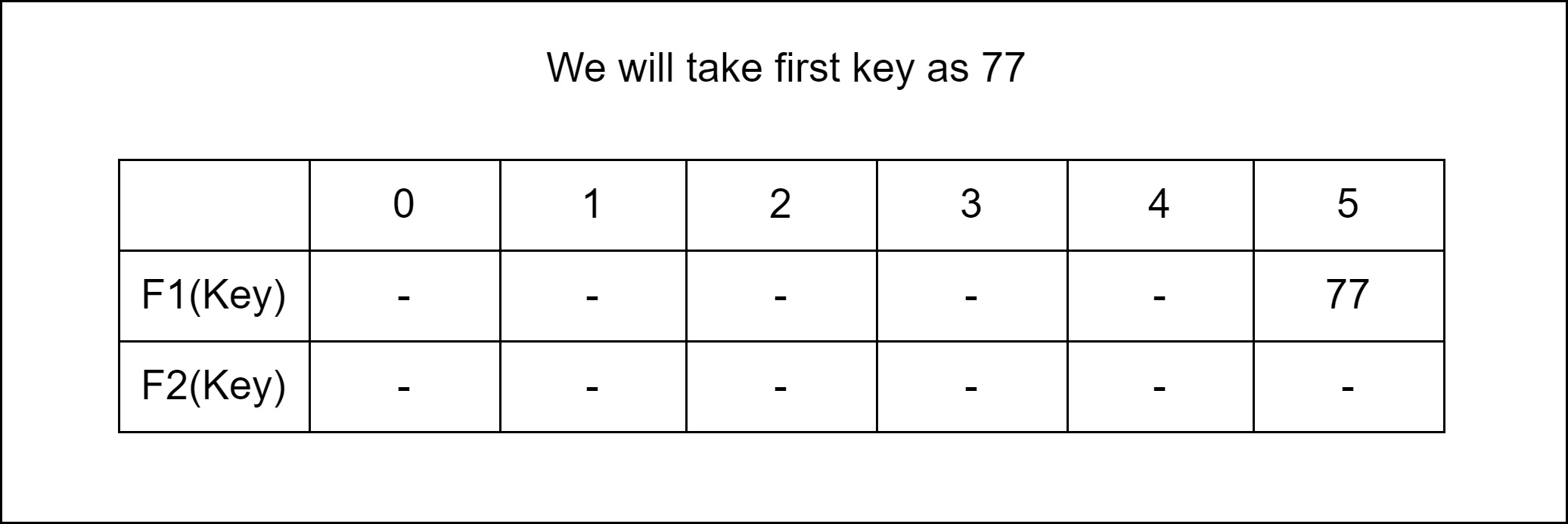
Multiple Choice: We are free to allow a choice for a Key to be inserted F1 (Key) and F2 (key).
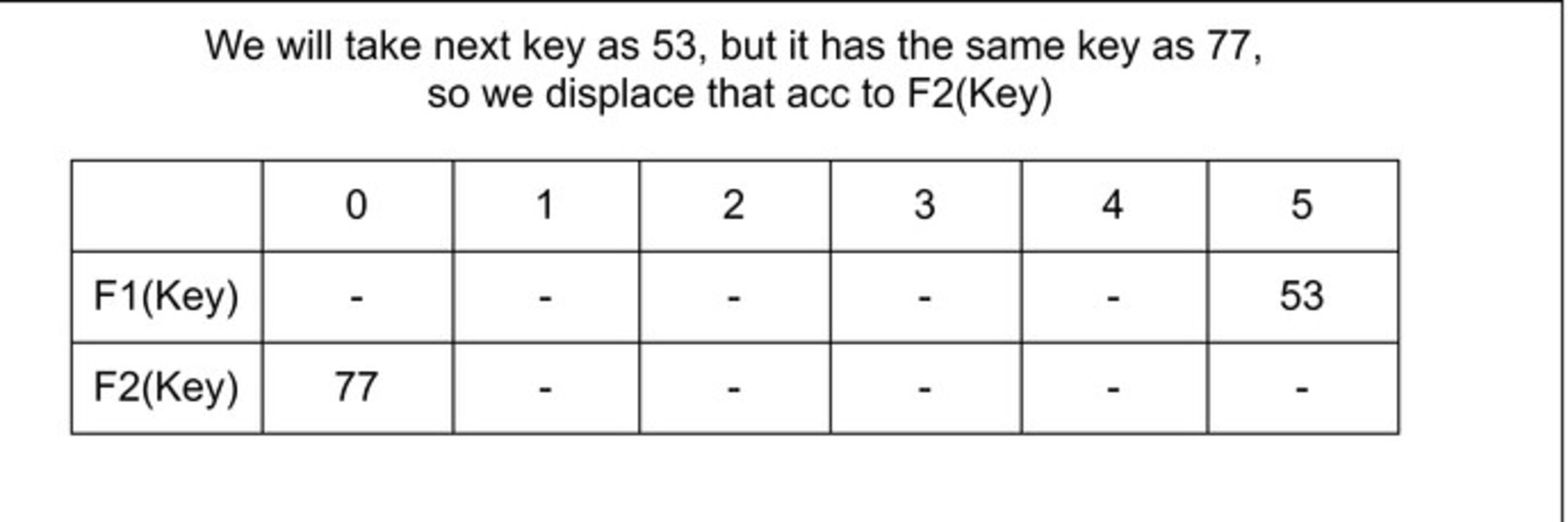
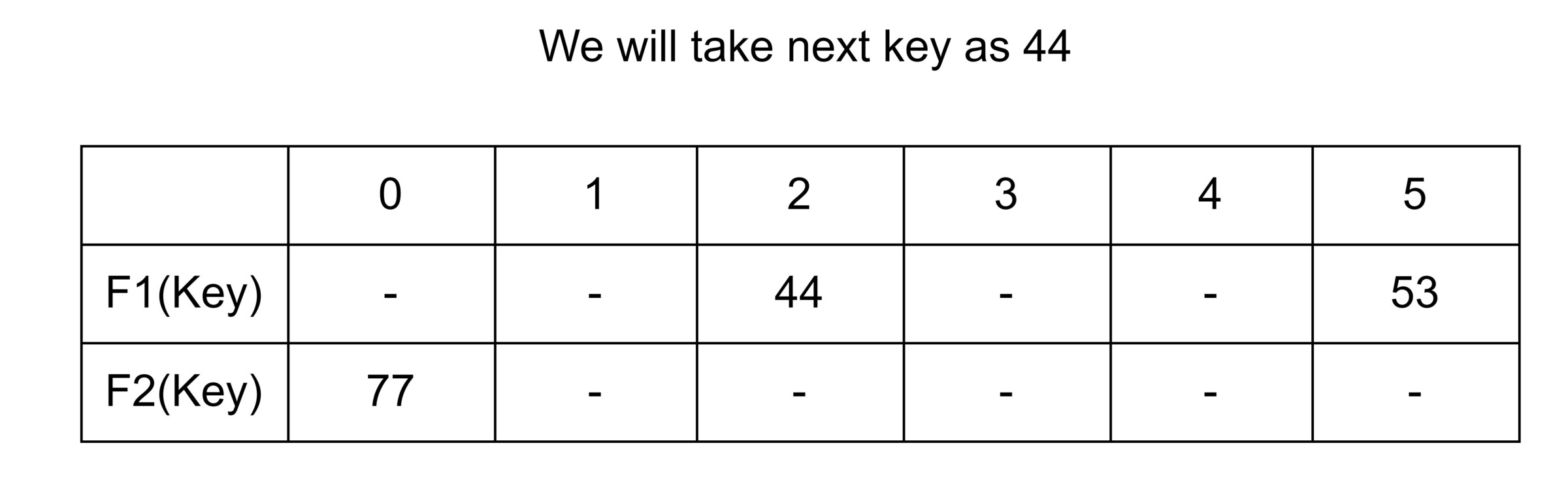
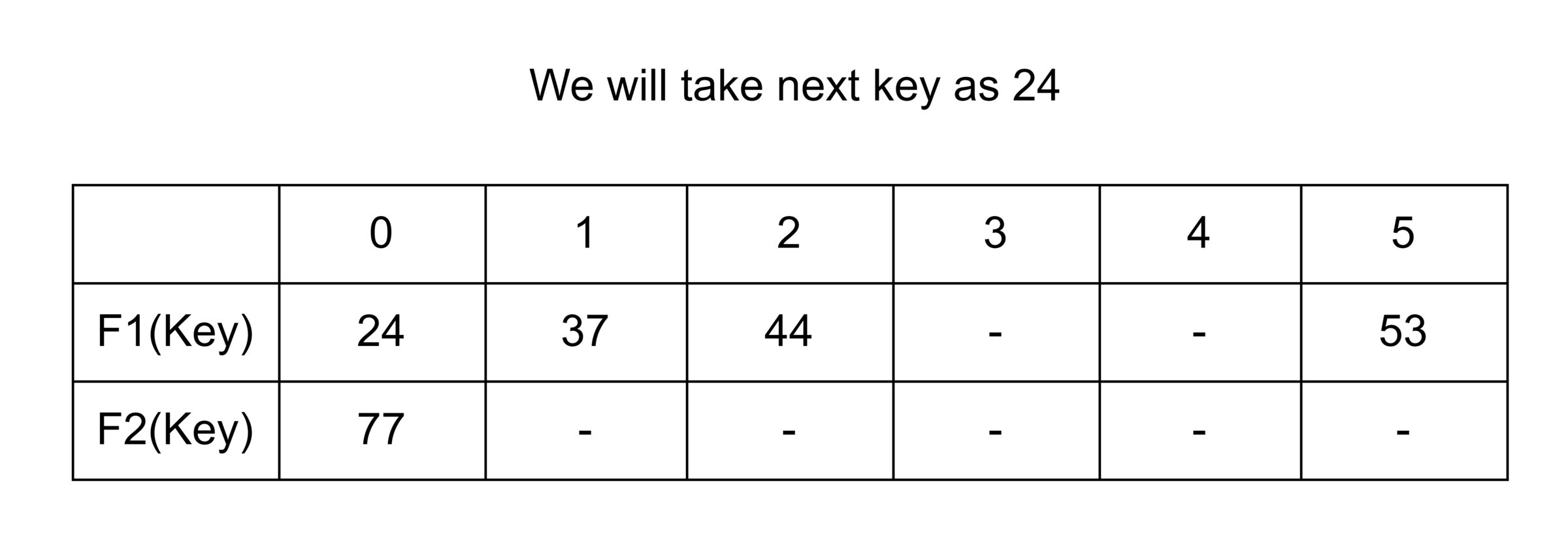
Relocation: A case is also possible that when F1 (Key) and F2 (key) both are occupied. So, it will try to copy the characteristic of a cuckoo bird, in a manner that pushing rest other eggs or the younger ones out of the nest. In a try to push a new key into the Hash Table. Then, it may push the older key to a new place. Now we have a problem to find a place for that older key.
Now two things are there. If a new place for that older key is an empty space, then it is good. But if it is not a vacant place, then…??
If this condition occurs then we have to displace that new key as well and find a new place for it. Now if again that condition occurs, then we just have to repeatedly displace the key to a new place until we find an empty of vacant space for the key.
Cuckoo Hashing – Worst case O(1)
Basically, there are 3 operations that supported by a Hash Table (or any suitable method In Languages) :
- Lookup(key): A Boolean function, Returns True/False if it is present or not.
- Insert(key): Make a new place and insert that item “Key” to the Hash Table if a new entry.
- Delete(key): Delete the “Key” from the Hash Table.





Code
C++ to implement Cuckoo Hashing
#include<bits/stdc++.h>
#define TNO 2
#define MOD 6
using namespace std;
int cuckooTable[TNO][MOD];
int POSITION[TNO];
void fillTable()
{
for (int j=0; j<MOD; j++)
for (int i=0; i<TNO; i++)
cuckooTable[i][j] = INT_MIN;
}
void printTable()
{
cout<<"Hash Tables are:\n"<<endl;
for (int i=0; i<TNO; i++, printf("\n"))
{
int k=i+1;
cout<<"Table: "<<k<<"-> ";
for (int j=0; j<MOD; j++)
{
if(cuckooTable[i][j]==INT_MIN)
cout<<" N ";
else
cout<<" "<<cuckooTable[i][j];
}
}
cout<<endl;
}
int getHashValue(int function, int key)
{
switch (function)
{
case 1:
return key%MOD;
case 2:
return (key/MOD)%MOD;
}
}
void getArrange(int key, int id, int c, int n)
{
if (c==n)
{
cout<<key<< " do not have a position\n"<<endl;
//cycle present rehash
return;
}
for (int i=0; i<TNO; i++)
{
POSITION[i] = getHashValue(i+1, key);
if (cuckooTable[i][POSITION[i]] == key)
return;
}
if (cuckooTable[id][POSITION[id]]!=INT_MIN)
{
int dis = cuckooTable[id][POSITION[id]];
cuckooTable[id][POSITION[id]] = key;
getArrange(dis, (id+1)%TNO, c+1, n);
}
else
cuckooTable[id][POSITION[id]] = key;
}
void cuckooFunction(int keys[], int n)
{
fillTable();
for (int i=0, c=0; i<n; i++, c=0)
getArrange(keys[i], 0, c, n);
printTable();
}
int main()
{
int keyTable1[] = {77, 53, 44, 37, 24, 55};
int n = sizeof(keyTable1)/sizeof(int);
cuckooFunction(keyTable1, n);
int keyTable2[] = {77, 53, 44, 37, 24, 55};
int m = sizeof(keyTable2)/sizeof(int);
cuckooFunction(keyTable2, m);
return 0;
}
Hash Tables are: Table: 1-> 24 55 44 N N 77 Table: 2-> 37 N 53 N N N Hash Tables are: Table: 1-> 24 55 44 N N 77 Table: 2-> 37 N 53 N N N
Cuckoo sequence program in Java
import java.util.*;
class CuckooHashing
{
private static int MOD = 6;
private static int TNO = 2;
private static int [][]cuckooTable = new int[TNO][MOD];
private static int []POSITION = new int[TNO];
public static void fillTable()
{
for (int j = 0; j < MOD; j++)
for (int i = 0; i < TNO; i++)
cuckooTable[i][j] = Integer.MIN_VALUE;
}
public static int getHashValue(int function, int key)
{
switch (function)
{
case 1:
return key % MOD;
case 2:
return (key / MOD) % MOD;
}
return Integer.MIN_VALUE;
}
public static void getArrange(int key, int id, int c, int n)
{
if (c == n)
{
System.out.println(key+" is not have a position");
return;
}
for (int i = 0; i < TNO; i++)
{
POSITION[i] = getHashValue(i + 1, key);
if (cuckooTable[i][POSITION[i]] == key)
return;
}
if (cuckooTable[id][POSITION[id]] != Integer.MIN_VALUE)
{
int dis = cuckooTable[id][POSITION[id]];
cuckooTable[id][POSITION[id]] = key;
getArrange(dis, (id + 1) % TNO, c + 1, n);
}
else
cuckooTable[id][POSITION[id]] = key;
}
public static void printTable()
{
System.out.println("Hash Tables are:");
for (int i = 0; i < TNO; i++, System.out.println())
{
int t=i+1;
System.out.print(" Table: " + t+" --> " );
for (int j = 0; j < MOD; j++)
{
if(cuckooTable[i][j] == Integer.MIN_VALUE)
System.out.print(" N ");
else
System.out.print(" "+ cuckooTable[i][j]);
}
System.out.println();
}
}
public static void cuckooFunction(int keys[], int n)
{
fillTable();
for (int i = 0, cnt = 0; i < n; i++, cnt = 0)
getArrange(keys[i], 0, cnt, n);
printTable();
}
public static void main(String[] args)
{
int KeysTable1[] = {77, 53, 44, 37, 24, 55};
int n = KeysTable1.length;
cuckooFunction(KeysTable1, n);
int KeysTable2[] = {77, 53, 44, 37, 24, 55};
int m = KeysTable2.length;
cuckooFunction(KeysTable2, m);
}
}Hash Tables are: Table: 1 --> 24 55 44 N N 77 Table: 2 --> 37 N 53 N N N Hash Tables are: Table: 1 --> 24 55 44 N N 77 Table: 2 --> 37 N 53 N N N
Complexity Analysis
Time Complexity
Insertion: O(1)
Deletion: O(1)
Space Complexity
O(1) as no extra space is required.