We are given an unsorted array. The task is to calculate the cumulative frequency of count of each element in an unsorted array.
Table of Contents
Example
Input:
A[]={2,4,3,2,2,3,4}Output:
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 3 in the array is: 5 Cumulative frequency of 4 in the array is: 7
Approach 1: Brute force
Main idea
For each element in the array, iterate the entire array and count the frequency of that element. Also, maintain a visited array that will store the elements we have already printed.
Algorithm
- Declare a visited array of the same size of the input array, where visited[i] is true if we have included ith element in the answer, otherwise false.
- Initialize a variable sum with 0, which will store the cumulative frequency of elements.
- Run a loop for I in range 0 to n-1
- If visited of I is false, initialize a count variable with zero, which will store the count of the current element
- Run a loop for j in range i to n-1
- If A[j] is equal to A[i], increment count by 1 and mark visited[j] as true
- Add count to sum.
- Print sum.
- Return
Implementation for Cumulative Frequency of Count of Each Element
C++ program
#include <bits/stdc++.h>
using namespace std;
void freq_of_elements(vector<int> A)
{
int n = A.size();
vector<bool> visited(n, false);
int sum = 0;
for (int i = 0; i < n; i++)
{
if (visited[i] == false)
{
int count = 0;
for (int j = i; j < n; j++)
{
if (A[i] == A[j])
{
count++;
visited[j] = true;
}
}
sum += count;
cout << "Cumulative frequency of " << A[i] << " in the array is: " << sum << endl;
}
}
return;
}
int main()
{
vector<int> A = {2, 4, 3, 2, 2, 3, 4};
freq_of_elements(A);
return 0;
}
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 4 in the array is: 5 Cumulative frequency of 3 in the array is: 7
JAVA program
public class Main
{
static void freq_of_elements(int A[])
{
int n = A.length;
int sum=0;
boolean visited[]= new boolean[n];
for (int i = 0; i < n; i++)
{
if (visited[i] == false)
{
int count = 0;
for (int j = i; j < n; j++)
{
if (A[i] == A[j])
{
count++;
visited[j] = true;
}
}
sum+=count;
System.out.println("Cumulative frequency of " + A[i] + " in the array is: " + sum);
}
}
}
public static void main(String[] args) {
int A[]= {2, 4, 3, 2, 2, 3, 4};
freq_of_elements(A);
}
}
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 4 in the array is: 5 Cumulative frequency of 3 in the array is: 7
Complexity Analysis for Cumulative Frequency of Count of Each Element
Time complexity
For each element, we are iterating the whole array, so the time complexity is O(N^2).
Space complexity
We are maintaining a visited array of size N, so the space complexity is O(N).
Approach 2: Using sorting
Main idea
We will first sort the array and then count the frequency of each element.
Algorithm
- Declare a variable count that will store the count.
- Initialize a variable count=1 which will store the count the current character.
- Declare a variable n that stores the size of the input array.
- Sort the input array.
- Run a loop for I in range 1 to n
- If I is equal to n or A[i] is not equal to A[i-1]
- Add count to sum, and print sum.
- Assign count=1.
- Else increment count by 1.
- If I is equal to n or A[i] is not equal to A[i-1]
- Return
Implementation for Cumulative Frequency of Count of Each Element
C++ program
#include <bits/stdc++.h>
using namespace std;
void freq_of_elements(vector<int> A)
{
sort(A.begin(), A.end());
int n = A.size();
int count = 1;
int sum = 0;
for (int i = 1; i <= n; i++)
{
if (i == n or A[i] != A[i - 1])
{
sum += count;
cout << "Cumulative frequency of " << A[i - 1] << " in the array is: " << sum << endl;
count = 1;
}
else
{
count++;
}
}
return;
}
int main()
{
vector<int> A = {2, 4, 3, 2, 2, 3, 4};
freq_of_elements(A);
return 0;
}
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 3 in the array is: 5 Cumulative frequency of 4 in the array is: 7
JAVA program
import java.util.Arrays;
public class Main
{
static void freq_of_elements(int A[])
{
Arrays.sort(A);
int n = A.length;
int sum=0;
int count=1;
for (int i = 1; i <= n; i++)
{
if (i == n || A[i] != A[i - 1])
{
sum+=count;
System.out.println("Cumulative frequency of " + A[i-1] + " in the array is: " + sum);
count=1;
}
else{
count++;
}
}
}
public static void main(String[] args) {
int A[]= {2, 4, 3, 2, 2, 3, 4};
freq_of_elements(A);
}
}
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 3 in the array is: 5 Cumulative frequency of 4 in the array is: 7
Complexity Analysis for Cumulative Frequency of Count of Each Element
Time complexity
Sorting the array takes O(N*logN) time and after that, we are traversing the array once. So total time complexity is O(N*logN+N) which is the same as O(N*logN).
Space complexity
We have not used any extra space, so space complexity is O(1).
Note: What if we need frequencies of elements according to the order of the first occurrence?
Approach 3: Using hashing
Main idea
We will store the frequency of each character in a hash table and after that, we will traverse the array and print the cumulative frequency of elements. After we print the cumulative frequency of an element, we will change its frequency in the hash table to zero so that we do not consider the same element twice.
Algorithm
- Initialize a hash table with zeros.
- Iterate over the input array and store the frequency of each element in the hash table.
- Initialize a variable sum with zero, which will store the cumulative frequency.
- Run a loop for i in range 0 to n-1
- If the value of A[i] in the hash table is not zero, add the frequency of A[i] to sum and print sum. Also change the frequency of A[i] to zero.
- Return.
Example
Input array:
A[]={2,4,3,2,2,3,4}
After iterating the input array, the hash table will look like this:
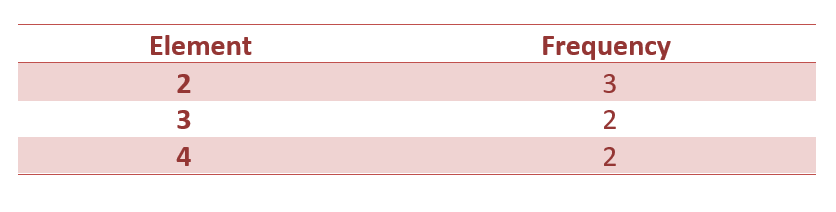
Implementation for Cumulative Frequency of Count of Each Element
C++ program
#include <bits/stdc++.h>
using namespace std;
void freq_of_elements(vector<int> A)
{
int n = A.size();
int sum = 0;
unordered_map<int, int> hash_table;
for (int i = 0; i < n; i++)
{
hash_table[A[i]]++;
}
for (int i = 0; i < n; i++)
{
if (hash_table[A[i]])
{
sum += hash_table[A[i]];
cout << "Cumulative frequency of " << A[i] << " in the array is: " << sum << endl;
hash_table[A[i]] = 0;
}
}
return;
}
int main()
{
vector<int> A = {2, 4, 3, 2, 2, 3, 4};
freq_of_elements(A);
return 0;
}
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 4 in the array is: 5 Cumulative frequency of 3 in the array is: 7
JAVA program
import java.util.Arrays;
public class Main
{
static void freq_of_elements(int A[])
{
java.util.HashMap<Integer, Integer> hash_table = new java.util.HashMap<Integer, Integer>();
int n = A.length;
int sum=0;
for(int i=0;i<n;i++)
{
Integer freq = hash_table.get(A[i]);
hash_table.put(A[i], (freq == null) ? 1 : freq + 1);
}
for (int i = 0; i < n; i++)
{
if (hash_table.get(A[i])!=0)
{
sum+=hash_table.get(A[i]);
System.out.println("Cumulative frequency of " + A[i] + " in the array is: " + sum);
hash_table.put(A[i], 0);
}
}
}
public static void main(String[] args) {
int A[]= {2, 4, 3, 2, 2, 3, 4};
freq_of_elements(A);
}
}
Cumulative frequency of 2 in the array is: 3 Cumulative frequency of 4 in the array is: 5 Cumulative frequency of 3 in the array is: 7
Complexity Analysis for Cumulative Frequency of Count of Each Element in an Unsorted Array
Time complexity
As we are iterating over the input array only twice, so the time complexity is O(N).
Space complexity
We are using a hash table to store the frequency of elements. So the space complexity is O(N).