Find sum of non-repeating elements (distinct) elements in an array

Problem Statement

Given an integer array, A[] with repeated elements, the “Find sum of non-repeating elements (distinct) elements in an array” problem asks to find the sum of all distinct elements in the array. So, simply add the numbers which are not repeated in the array.

Example

A[]={1, 4, 2, 1, 5, 2, 3, 2}

11

Explanation: Non-repeating elements are: 4, 5, 3. So their sum=4+5+3=11.

Brute force

Main idea to find sum of non-repeating elements (distinct) elements in an array

For every element, check if there is another element present or not whose value is the same and has an index less than the current index. If there is no such element, add the current element to the answer otherwise skip it.

Algorithm

1. Run a loop for I in range 0 to n-1 
    1. Run a loop for j in range 0 to i 
        1. If j==i, add A[i]. 
        2. If A[i] is equal to A[j], break out from this loop. 
    2. Return.

Code

C++ code

#include <bits/stdc++.h>
using namespace std;
void sumOfDistinctElements(vector<int> A)
{
    int n = A.size();
    int sum = 0;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
        {
            if (j == i)
            {
                sum += A[i];
            }
            if (A[i] == A[j])
            {
                break;
            }
        }
    }
    cout << "Sum of distinct Elements in the array is: " << sum << endl;
    return;
}
int main()
{
    vector<int> A = {1, 4, 2, 1, 5, 2, 3, 2};
    sumOfDistinctElements(A);
    return 0;
}

Sum of distinct Elements in the array is: 15

Java code

public class Main
{   
    static void sumOfDistinctElements(int A[])
    {
        int n = A.length;
        int sum = 0;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j <= i; j++)
            {
                if (j == i)
                {
                    sum += A[i];
                }
                if (A[i] == A[j])
                {
                    break;
                }
            }
        }
        System.out.println("Sum of distinct Elements in the array is: " + sum);
        return;
    }
  public static void main(String[] args) {
    int A[] = {1, 4, 2, 1, 5, 2, 3, 2};
        sumOfDistinctElements(A);
  }
}

Sum of distinct Elements in the array is: 15

Complexity Analysis

Time complexity

We have two nested loops, each of size n. So the time complexity is O(N^2).

Space complexity

We are not taking any extra space so the space complexity is O(1).

Optimized Approach

Main idea to find sum of non-repeating elements (distinct) elements in an array

We will maintain a hash table which will store the elements we have already printed. So, we will iterate the array, if we have found an element in the array which is not present in the hash table then we will add that element to the answer and insert it in the hash table, otherwise we will skip that element.

Algorithm

1. Declare a hash table.
2. Run a loop for I in range 0 to n-1:
    1. If A[i] is not present in the hash table, then add it and insert it in the hash table.
    2. If A[i] is not present in the hash table then skip it.
3. Return.

Example

Let’s say

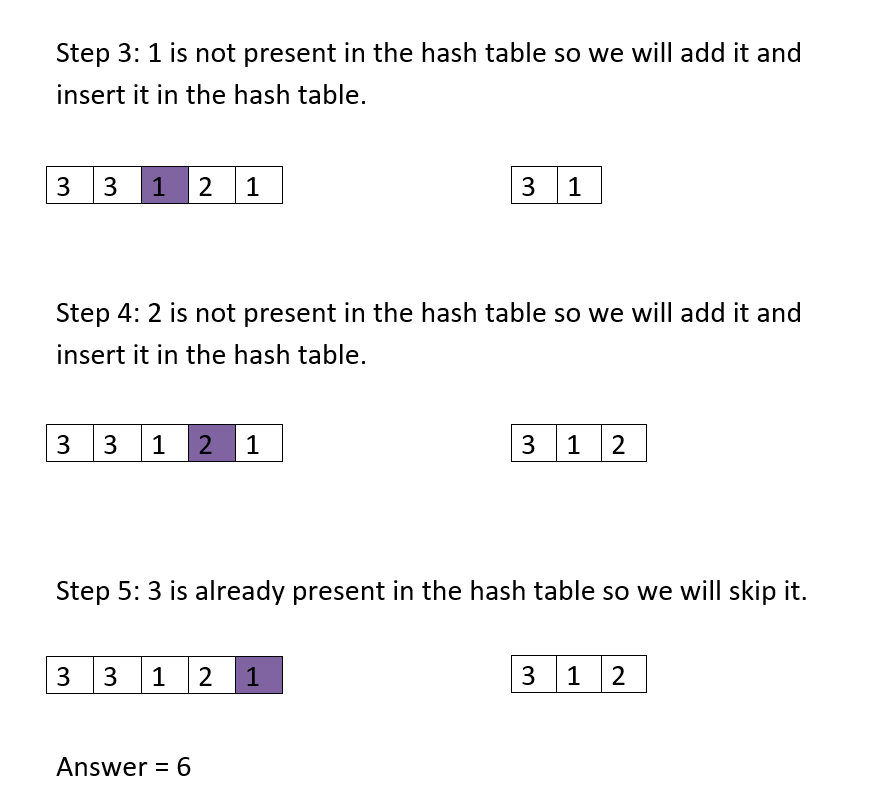
A[]={3, 3, 1, 2 ,1}

The table on the left side is our input array and purple color points to the current index.

The table on the right is the hash table

Code

C++ code

#include <bits/stdc++.h>
using namespace std;
void sumOfDistinctElements(vector<int> A)
{
    int n = A.size();
    int sum = 0;
    unordered_set<int> hash_table;
    for (int i = 0; i < n; i++)
    {
        if (hash_table.count(A[i]) == 0) //hash_table.count(x) returns 1 if x is present in the hash_table otherwise returns 0
        {
            hash_table.insert(A[i]);
            sum += A[i];
        }
    }
    cout << "Sum of distinct Elements in the array is: " << sum << endl;
    return;
}
int main()
{
    vector<int> A = {1, 4, 2, 1, 5, 2, 3, 2};
    sumOfDistinctElements(A);
    return 0;
}

Sum of distinct Elements in the array is: 15

Java code

import java.util.*;
public class Main
{   
    static void sumOfDistinctElements(int A[])
    {
        int n = A.length;
        int sum = 0;
        HashSet<Integer> hash_table = new HashSet<Integer>(); 
        for (int i = 0; i < n; i++) 
        { 
            if (!hash_table.contains(A[i])) 
            { 
                sum += A[i]; 
                hash_table.add(A[i]); 
            } 
        } 
        System.out.println("Sum of distinct Elements in the array is: " + sum);
        return;
    }
  public static void main(String[] args) {
    int A[] = {1, 4, 2, 1, 5, 2, 3, 2};
        sumOfDistinctElements(A);
  }
}

Sum of distinct Elements in the array is: 15

Complexity Analysis

Time complexity

We iterate the array only once and the time complexity of insert function in unordered set is O(1), so total time complexity is O(N).

Space complexity

We took an extra hash table so our space complexity is O(N).