Minimum swaps required to bring all elements less than or equal to k together

The problem “Minimum swaps required to bring all elements less than or equal to k together” states that you have an integer array. The problem statement asks to find out the smallest count of swaps that will be required to get the elements together which are less than or equal to the given number k.

Example

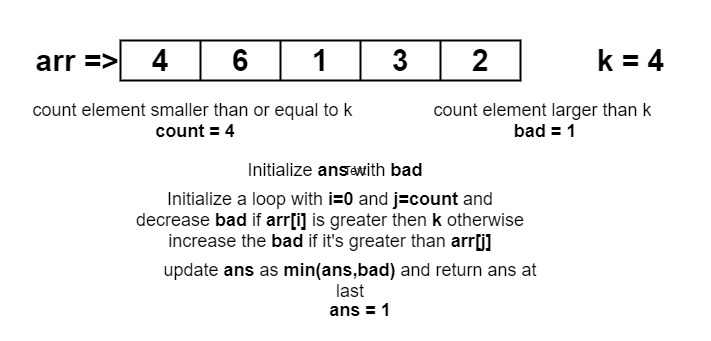
arr[]={4,6,1,3,2}, k = 4

1

Explanation

Only 1 swap is required. 6 can be swapped with 2 so that 4, 2, 1, and 3 come together.

Algorithm

1. Get the count of all the elements which are less than equal to k.
2. Get the count of all the elements which are greater than k.
3. Set output to the value of smaller.
4. Traverse the array from i = 0 and j = count.
   1. Check if array[ i ] is greater than the value of k, then, decrease the value of smaller by 1.
   2. Check if array[ j ] is greater than the value of k, then, increase the value of smaller by 1.
   3. Find out the minimum between the output and the smaller and store it to output.
5. Return the value of output.

Explanation

We have given an array of integers, and an integer value called k, we have asked to find out how many minimum swaps are required to get all the elements together which are less than or equal to k. Remember we only need to find the minimum swaps.

For that, we are going to count the number of elements which are less than or equal to k, and store it to smaller variable. So smaller variable will hold the count of smaller number which are less than or equal to k. Similar to that count, we count all the numbers which are greater than the number k. Set the value of output to smaller, later on, we will be comparing the values with this output and keep on storing in it simultaneously. If we take an example which was mentioned above, 4 is the count of smaller, and 1 is the count of greater.

Traverse the array with taking i = 0, j = smaller, check array[i] and arr[j] is greater than the value of k, if arr[i] is greater then, decrease the count of smaller if array[j] is greater then increase the count of smaller.

Simultaneously we will find out the minimum between the output and smaller number, in the loop we are traversing we are doing both of the operations, to decrease the value of smaller and to increase the value of smaller. At last, we just have to return the value of output. Because it will be having the desired output.

Code

C++ code to find minimum swaps required to bring all elements less than or equal to k together

#include <iostream>

using namespace std;

int minimumSwapToK(int arr[], int n, int k)
{
    int count = 0;
    for (int i = 0; i < n; ++i)
        if (arr[i] <= k)
            ++count;

    int bad = 0;
    for (int i = 0; i < count; ++i)
        if (arr[i] > k)
            ++bad;

    int ans = bad;
    for (int i = 0, j = count; j < n; ++i, ++j)
    {

        if (arr[i] > k)
            --bad;

        if (arr[j] > k)
            ++bad;

        ans = min(ans, bad);
    }
    return ans;
}

int main()
{
    int arr[] = {4,6,1,3,2};
    int n = sizeof(arr) / sizeof(arr[0]);
    int k = 4;
    int result = minimumSwapToK(arr, n, k);
    cout <<result;
    return 0;
}

1

Java code to find minimum swaps required to bring all elements less than or equal to k together

class minimumSwaps
{
    public static int minimumSwapToK(int arr[], int n, int k)
    {

        int count = 0;
        for (int i = 0; i < n; ++i)
            if (arr[i] <= k)
                ++count;

        int bad = 0;
        for (int i = 0; i < count; ++i)
            if (arr[i] > k)
                ++bad;

        int ans = bad;
        for (int i = 0, j = count; j < n; ++i, ++j)
        {

            if (arr[i] > k)
                --bad;

            if (arr[j] > k)
                ++bad;

            ans = Math.min(ans, bad);
        }
        return ans;
    }
    public static void main(String[] args)
    {
        int arr[] = {4,6,1,3,2};
        int n = arr.length;
        int k = 4;
        int result = minimumSwapToK(arr, n, k);
        System.out.println(result);

    }
}

1

Complexity Analysis

Time Complexity

O(n) where “n” is the number of elements in the array. Because we had run loops that did not have nested loops. Thus the time complexity is linear.

Space Complexity

O(1) as no extra space is required. So the space complexity is constant.