Table of Contents
Problem Statement
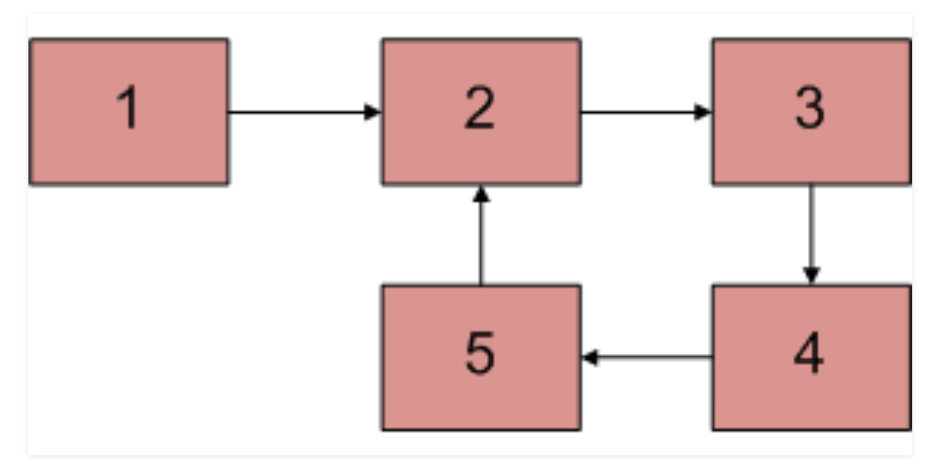
In the “Detect a loop in the Linked List” problem we have given a linked list. Find whether there is loop or not. If there is a loop in the linked list then some node in the linked list will be pointing to one of the previous nodes in the same linked list.
Example
1 2 3 4 5
1 2 3 4 5
Approach
We will use the Tortoise and Hare approach where two pointers are maintained to solve this problem.
- Slow pointer( tortoise) //Moves only 1 step at a time
- Fast Pointer(hare) //Moves 2 steps at a time
At each iteration, we move one of the pointers by two steps and the other one by one step. So you have two pointers tortoise and the hare.
By this algorithm the two cases arise:
- Hare will reach the end of the linked list(null), which means that there is no cycle in it.
- Hare will meet the tortoise, which means that there is a cycle in the linked list.
In each step, the tortoise walks 1 node and the hare walks 2 nodes. The tortoise gets away by 1 distance unit, and then the hare gets nearby 2 distance units. it’s just like in each step, the tortoise stays stationary and the hare moves by 1 step.
Proof
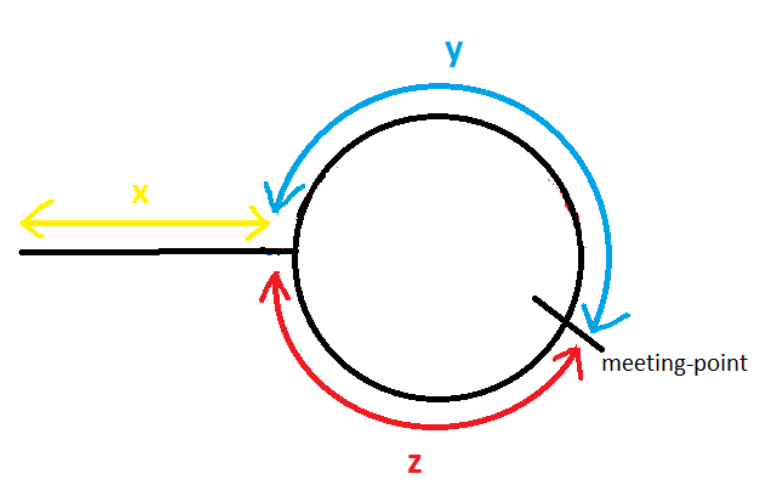
The loop length, n =y+z
Distance travelled by slowPointer(tortoise) before meeting= x + c1*n +y
Distance travelled by fastPointer(hare) before meeting = x + c2*n + y
Where c1 and c2 are constants. Since fastPointer(hare) travels with double the speed of slow pointer(tortoise), and time is constant for both when they reach the meeting point. So,
2(x+c1*n+y) = x+c2*n
=> x+y = (2*c1 – c2)*n => x + y = K*n (K is a constant) => x = K*n – y => x = z
So by moving the slowpointer to start of a linked list, and making both slowPointer and fastPointer move one node at a time, they both will reach the point where the loop starts in the linked list.
Implementation
C++ Program to Detect a loop in the Linked List
#include<bits/stdc++.h>
using namespace std;
class MyLinkedList {
public:
struct ListNode {
ListNode *next;
int val;
ListNode(int a): next(NULL), val(a){}
};
ListNode *head;
MyLinkedList():head(NULL) {
}
void addAtHead(int val) {
ListNode *node = new ListNode(val);
node->next = head;
head = node;
}
bool hasCycle() {
ListNode *slow=head,*fast=head;
while(fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if(slow==fast)
return true;
}
return false;
}
void print_list(){
ListNode* node = head;
while(node){
cout<<node->val<<" ";
node = node->next;
}
cout<<endl;
}
};
int main(){
MyLinkedList *list = new MyLinkedList();
list->addAtHead(10);
list->addAtHead(7);
list->addAtHead(4);
cout<<list->hasCycle();
}Java Program to Detect a loop in the Linked List
import java.util.*;
import java.lang.*;
import java.io.*;
public class Main{
public static void main (String[] args) throws java.lang.Exception{
MyLinkedList obj = new MyLinkedList();
obj.addAtHead(10);
obj.addAtHead(7);
obj.addAtHead(4);
System.out.println(obj.hasCycle());
}
public static class MyLinkedList {
class Node{
Node next = null;
int val = 0;
public Node(int val){
this.val = val;
}
}
private Node head;
private int size;
public MyLinkedList() {
this.head = null;
this.size = 0;
}
public Node getNodeAt(int index){
Node curr = head;
while(index-- > 0){
curr = curr.next;
}
return curr;
}
public void addAtHead(int val) {
Node node = new Node(val);
if(this.size == 0){
this.head = node;
}
else{
node.next = this.head;
this.head = node;
}
this.size++;
}
public boolean hasCycle() {
if(head==null || head.next==null) return false;
Node fast=head,slow=head;
while(fast!=null && fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if(fast==slow) return true;
}
return false;
}
public void printList(){
Node curr = head;
while(curr!=null){
System.out.print(curr.val+" ");
curr = curr.next;
}
System.out.println("");
}
}
}Complexity Analysis to Detect a loop in the Linked List
Time Complexity
O(n) where n is the number of nodes present in the linked list. Here we traverse the linked list and check for loop which take linear time.
Space Complexity
O(1) because we don’t use any auxiliary space here.