Table of Contents
Problem Statement
The problem “Implementation of Deque using Doubly Linked List” states that you need to implement the following functions of Deque or Doubly Ended Queue using a doubly linked list,
- insertFront(x) : Add element x at the starting of Deque
- insertEnd(x) : Add element x at the end of Deque
- deleteFront() : Delete an element from the starting of Deque
- deleteEnd() : Delete an element from the end of Deque
- getFront() : Return the element at the starting of Deque
- getEnd() : Return the element at the end of Deque
- isEmpty() : Returns whether the Deque is empty
- size() : Return the size of Deque
- erase() : Delete all the elements of Deque
Example
insertFront(5) insertEnd(10) insertEnd(11) insertFront(19) getFront() getEnd() deleteEnd() getEnd() deleteFront() getFront() size() isEmpty() erase() isEmpty()
19 11 10 5 2 false true
Algorithm
To implement a Deque using a doubly linked list. We maintain two pointers front and rear, where front points to the front of a doubly linked list and rear points to the end. Also we need to maintain an integer size, that stores the number of nodes in the Deque.
To insert, delete, or get an element from starting we use the front pointer.
To insert, delete, or get an element from the end we use the rear pointer.
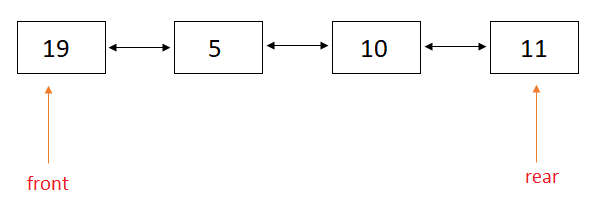
insertFront(x)
To insert an element at the front of Deque, do the following
- Create a new node with the required value and call it node.
- If the front is null, make the front and rear equals node.
- Else, insert the node before front and mark the node as a new front.
- Increment size
Time Complexity O(1)
Pseudo Code
Create a new node with required value and call it node
if (front == null) {
front = rear = node
} else {
node.next = front
front.prev = node
front = node
}
size++insertEnd(x)
To insert an element at the end of Deque, do the following
- Create a new node with required value and call it node.
- If rear is null, make front and rear equals node.
- Else, insert node after rear and mark the node as new rear.
- Increment size
Time Complexity O(1)
Pseudo Code
Create a new node with required value and call it node
if (rear == null) {
front = rear = node
} else {
rear.next = node
node.prev = rear
rear = node
}
size++deleteFront()
To delete an element from front of Deque, do the following
- If front is null, there is no element to delete, simply return.
- If front is equals to rear, there is only 1 node, make front and rear null.
- Else, make front equals front.next and delete front.prev
- Decrement size
Time Complexity = O(1)
Pseudo Code
if (front == null) {
return
}
if (front == rear) {
front = rear = null
} else {
temp = front
front = front.next
front.prev = null
deallocate space for temp
}
size--deleteEnd()
To delete an element from the end of Deque, do the following
- If rear is null, there is no node to delete, simply return.
- If rear is equals to front, there is only one node, make front and rear null.
- Else make rear as rear.prev and delete rear.next.
- Decrement size
Time Complexity = O(1)
Pseudo Code
if (rear == null) {
return;
}
if (rear == front) {
front = rear = null
} else {
temp = rear
rear = rear.prev
rear.next = null
deallocate space for temp
}
size--getFront()
The front element of the Deque is pointed by front, so if front is not null return front.data
Time Complexity = O(1)
Pseudo Code
if (front != null) {
return front.data
}
return -1getEnd()
The end element of Deque is pointed by rear, so if rear is not null return rear.data
Time Complexity = O(1)
Pseudo Code
if (rear != null) {
return rear.data
}
return -1isEmpty()
If the Deque is empty both front and rear will be null, so if front is null return true, else return false.
Time Complexity = O(1)
Pseudo Code
if (front == null) {
return true
}
return falsesize()
The size of the Deque is stored in the variable named ‘size’, so simply return size.
Time Complexity = O(1)
Pseudo Code
return size
erase()
Erasing Deque means deleting all the nodes of the Deque. To delete all the nodes do the following,
- Set rear as null.
- Create a temporary pointer temp, pointing to front.
- Traverse in the Deque and repeat step 4, that is, while front is not null repeat step 4.
- Set temp as front, front as front.next and deallocate space for temp.
- Finally set temp as null and front as null and set size as 0.
Time Complexity = O(n), where n is the number of nodes in the Deque
Pseudo Code
rear = null
Node temp = front
while (front != null) {
temp = front
front.prev = null
front = front.next
deallocate space for temp
}
temp = front = null
size = 0Code
Java code for Implementation of Deque using Doubly Linked List
class DequeUsingDoublyLinkedList {
// class representing Node of a doubly linked list
static class Node {
int data;
Node next, prev;
public Node(int data) {
this.data = data;
}
}
// front points to start of Deque and rear points to the end of Deque
private static Node front = null;
private static Node rear = null;
private static int size = 0;
private static void insertFront(int x) {
// Create a new Node with required parameters
Node node = new Node(x);
if (front == null) {
// This is the first node to be inserted
front = rear = node;
} else {
// Add the node before front
node.next = front;
front.prev = node;
// update front
front = node;
}
// Increment size
size++;
}
private static void insertEnd(int x) {
// Create a new Node with required parameters
Node node = new Node(x);
if (rear == null) {
// This is the first node to be inserted
front = rear = node;
} else {
// Insert the node after rear
rear.next = node;
node.prev = rear;
// update rear
rear = node;
}
// Increment size
size++;
}
private static void deleteFront() {
if (front == null) {
// no node to delete
return;
}
if (front == rear) {
// only 1 node is present
front = rear = null;
} else {
// delete front and move front ahead
front = front.next;
front.prev = null;
// Garbage Collector will automatically delete first node
// as no pointer is pointing to it
}
// decrement size
size--;
}
private static void deleteEnd() {
if (rear == null) {
// no node to delete
return;
}
if (rear == front) {
// only 1 node is present
front = rear = null;
} else {
// delete rear and move rear backwards
rear = rear.prev;
rear.next = null;
// Garbage Collector will automatically delete last node
// as no pointer is pointing to it
}
// decrement size
size--;
}
private static int getFront() {
if (front != null) {
// front points to first element in Deque, return its data
return front.data;
}
// no node is present
return -1;
}
private static int getEnd() {
if (rear != null) {
// rear points to last element in Deque, return its data
return rear.data;
}
// no node is present
return -1;
}
private static boolean isEmpty() {
if (front == null) {
return true;
}
return false;
}
private static int size() {
return size;
}
private static void erase() {
// mark rear as null
rear = null;
// traverse the doubly linked list
while (front != null) {
// delete all the prev pointers
front.prev = null;
front = front.next;
}
// After this deque looks like
// a -> b -> c -> d ..., all the previous pointers are destroyed
// No pointer is pointing to a, so Garbage collector will delete the whole Deque
// set size as 0
size = 0;
}
public static void main(String[] args) {
// Example
insertFront(5); // 5
insertEnd(10); // 5 <-> 10
insertEnd(11); // 5 <-> 10 <-> 11
insertFront(19); // 19 <-> 5 <-> 10 <-> 11
System.out.println(getFront());
System.out.println(getEnd());
deleteEnd(); // 19 <-> 5 <-> 10
System.out.println(getEnd());
deleteFront(); // 5 <-> 10
System.out.println(getFront());
System.out.println(size());
System.out.println(isEmpty());
erase();
System.out.println(isEmpty());
}
}19 11 10 5 2 false true
C++ Code for Implementation of Deque using Doubly Linked List
#include<bits/stdc++.h>
using namespace std;
// class representing a tree node
class Node {
public:
int data;
Node *next;
Node *prev;
Node(int d) {
data = d;
next = NULL;
prev = NULL;
}
};
// function to create a new node
Node* newNode(int x) {
Node *node = new Node(x);
return node;
}
// front points to start of Deque and rear points to the end of Deque
Node *front = NULL;
Node *rear = NULL;
// Variable representing size of Deque
int Size = 0;
void insertFront(int x) {
// Create a new Node with required parameters
Node *node = newNode(x);
if (front == NULL) {
// This is the first node to be inserted
front = rear = node;
} else {
// Add the node before front
node->next = front;
front->prev = node;
// update front
front = node;
}
// Increment size
Size++;
}
void insertEnd(int x) {
// Create a new Node with required parameters
Node *node = newNode(x);
if (rear == NULL) {
// This is the first node to be inserted
front = rear = node;
} else {
// Insert the node after rear
node->prev = rear;
rear->next = node;
// update rear
rear = node;
}
// Increment size
Size++;
}
void deleteFront() {
if (front == NULL) {
// no node to delete
return;
}
if (front == rear) {
// only 1 node is present
front = rear = NULL;
} else {
// delete front and move front ahead
Node *temp = front;
front = front->next;
front->prev = NULL;
// deallocate the memory taken by temp
delete(temp);
}
// Decrement size
Size--;
}
void deleteEnd() {
if (rear == NULL) {
// no node to delete
return;
}
if (front == rear) {
// only 1 node is present
front = rear = NULL;
} else {
// delete rear and move rear backwards
Node *temp = rear;
rear = rear->prev;
rear->next = NULL;
// deallocate the memory taken by temp
delete(temp);
}
// Decrement size
Size--;
}
int getFront() {
if (front != NULL) {
return front->data;
}
return -1;
}
int getEnd() {
if (rear != NULL) {
return rear->data;
}
return -1;
}
int size() {
return Size;
}
bool isEmpty() {
if (front == NULL) {
return true;
}
return false;
}
void erase() {
// mark rear as null
rear = NULL;
// traverse the doubly linked list
while (front != NULL) {
Node *temp = front;
// delete all the prev pointers
front->prev = NULL;
front = front->next;
// Deallocate the memory taken by temp
delete(temp);
}
// Set size as 0
Size = 0;
}
int main() {
// Example
insertFront(5); // 5
insertEnd(10); // 5 <-> 10
insertEnd(11); // 5 <-> 10 <-> 11
insertFront(19); // 19 <-> 5 <-> 10 <-> 11
cout<<getFront()<<endl;
cout<<getEnd()<<endl;
deleteEnd(); // 19 <-> 5 <-> 10
cout<<getEnd()<<endl;
deleteFront(); // 5 <-> 10
cout<<getFront()<<endl;
cout<<size()<<endl;
if (isEmpty()) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
erase();
if (isEmpty()) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}19 11 10 5 2 false true