Merge K sorted linked lists problem is so famous as per the interview point of view. This question asks so many times in big companies like Google, Microsoft, Amazon, etc. As the name suggests we’ve been provided with k sorted linked lists. We have to merge them together into a Single Sorted Linked List.
Let’s look into a sample test case to understand it better:
Table of Contents
Example
Input
[
1->2->3,
1->4->6,
2->3
]
Output
1->1->2->2->3->3->4->6
Approach-1 for Merge K Sorted Linked Lists
Brute Force
- Traverse all the linked lists and put all the values in an Array/ArrayList/Vector(Whatever storage you find convenient)
- Sort the data
- Create a new linked list from the sorted data
Voila!our merged and sorted linked list is ready. Let’s understand that better by a code.
Java Program
class Solution
{
public ListNode mergeKLists(ListNode[] lists)
{
ListNode aux=new ListNode(0);
List<Integer>lisa=new ArrayList<Integer>();
for(int i=0;i<lists.length;i++)
{
ListNode ptr=lists[i];
while(ptr!=null)
{
lisa.add(ptr.val);
ptr=ptr.next;
}
}
Collections.sort(lisa);
ListNode ptr=aux;
for(int i=0;i<lisa.size();i++)
{
ListNode temp=new ListNode(lisa.get(i));
temp.next=null;
ptr.next=temp;
ptr=ptr.next;
}
return aux.next;
}
}C++ Program
class Solution
{
public:
ListNode* mergeKLists(vector<ListNode*>& lists)
{
vector<int>store;
for(int i=0;i<lists.size();i++)
{
ListNode *ptr=lists[i];
while(ptr!=NULL)
{
store.push_back(ptr->val);
ptr=ptr->next;
}
}
sort(store.begin(),store.end());
ListNode *ptr=new ListNode();
ListNode *aux=ptr;
for(int i=0;i<store.size();i++)
{
ListNode *temp=new ListNode(store[i]);
temp->next=NULL;
ptr->next=temp;
ptr=ptr->next;
}
return aux->next;
}
};[ 1->2->3, 1->4->6, 2->3 ]
1->1->2->2->3->3->4->6
Complexity Analysis
Let us now look into the time complexity of the above solution:
The time is taken for traversal and creation: O(n)
The time is taken for sorting: O(n log n)
Making the time complexity: O(n log n)
Approach-2 for Merge K Sorted Linked Lists
Using Min-Heap
A Priority Queue can be used as a storage
Advantages:
- No need for sorting
Let’s look into the same with the help of a code
Java Program
class Solution
{
public ListNode mergeKLists(ListNode[] lists)
{
Queue<Integer>store=new PriorityQueue();
for(int i=0;i<lists.length;i++)
{
ListNode ptr=lists[i];
while(ptr!=null)
{
store.add(ptr.val);
ptr=ptr.next;
}
}
if(store.isEmpty() )
return null;
ListNode head=new ListNode(store.poll());
ListNode cur=head;
while(!store.isEmpty())
{
ListNode temp=new ListNode(store.poll());
cur.next=temp;
cur=cur.next;
}
return head;
}
}[ 2->5->7->9, 1->2->3->->10 ]
1->2->2->3->5->7->9->10
Complexity Analysis
The time complexity of the above: O(n log n)
Approach-3 for Merge K Sorted Linked Lists
Divide and Conquer
- The Divide step
OBJECTIVE-Sends k lists to merge function k/2 at time
- The Merge step
OBJECTIVE-To consider smaller values and add them to create a new list
- Create a pointer to return the combined list
- Add the smaller value from either list
- Increment pointer from which value has been taken
- Return merged and sorted linked list from two lists
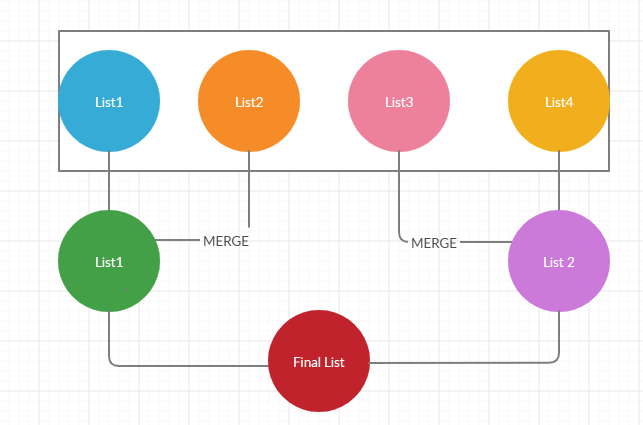
Let’s understand that better with the help of code
Java Program
class Solution
{
public static ListNode merge(ListNode l1,ListNode l2)
{
if(l1==null)
return l2;
if(l2==null)
return l1;
ListNode aux=new ListNode();
ListNode head=aux;
while(l1!=null && l2!=null)
{
if(l1.val>l2.val)
{
aux.next=l2;
l2=l2.next;
}
else
{
aux.next=l1;
l1=l1.next;
}
aux=aux.next;
}
if(l1!=null)
aux.next=l1;
else if(l2!=null)
aux.next=l2;
return head.next;
}
public static ListNode divide(ListNode[]lists,int start,int end)
{
if(end<start)
return null;
if(end==start)
return lists[start];
int mid=start+(end-start)/2;
return(merge(divide(lists,start,mid),divide(lists,mid+1,end)));
}
public ListNode mergeKLists(ListNode[] lists)
{
if(lists == null)
return null;
if(lists.length == 1)
return lists[0];
return divide(lists,0,lists.length-1);
}
}C++ Program
class Solution
{
public:
ListNode* merge(ListNode *l1,ListNode *l2)
{
if(l1==NULL)
return l2;
if(l2==NULL)
return l1;
ListNode *aux=new ListNode();
ListNode *head=aux;
while(l1!=NULL && l2!=NULL)
{
if(l1->val>l2->val)
{
aux->next=l2;
l2=l2->next;
}
else
{
aux->next=l1;
l1=l1->next;
}
aux=aux->next;
}
if(l1!=NULL)
aux->next=l1;
else if(l2!=NULL)
aux->next=l2;
return head->next;
}
public:
ListNode* divide(vector<ListNode*>&lists,int start,int end)
{
if(end<start)
return NULL;
if(end==start)
return lists[start];
int mid=start+(end-start)/2;
return(merge(divide(lists,start,mid),divide(lists,mid+1,end)));
}
public:
ListNode* mergeKLists(vector<ListNode*>& lists)
{
if(lists.size() == 0)
return NULL;
if(lists.size() == 1)
return lists[0];
return divide(lists,0,lists.size()-1);
}
};[ 1->2, 3, 4->5->6->7, 8->9->10, 11 ]
1->2->3->4->5->6->7->8->9->10->11
Complexity Analysis
The time complexity=O(n log n)
The space complexity=O(1)