In the minimum path sum problem, we have given “a × b” matrix consisting of non-negative numbers. Your task is to find the path from top left to right bottom which minimizes the sum consisting of all the numbers which come in a path you found.
Note: You can only move either down or right at any point in time.
Table of Contents
Example
Input
[1,0,2],
[2,0,5],
[1,0,1]
Output
2
Explanation
Because it follows the path 1→0→0→0→1, which minimizes the sum as 2.
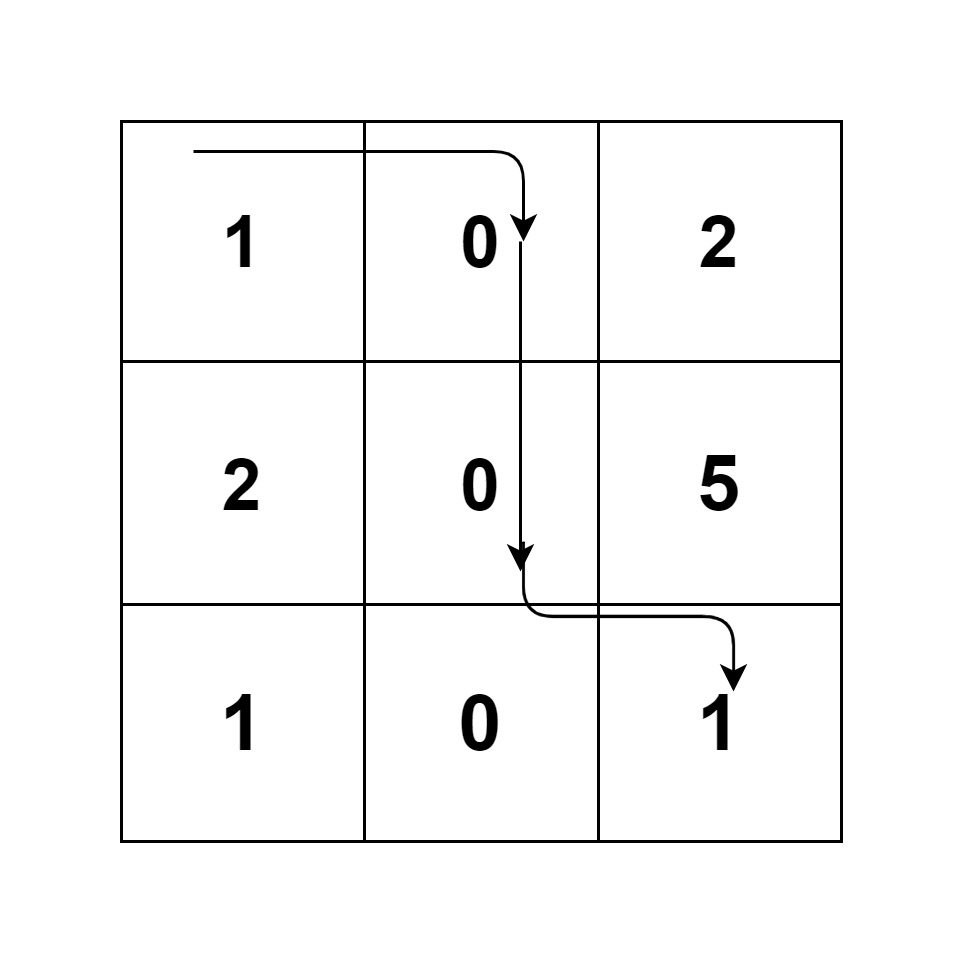
This image shows the path followed to reach from top left to bottom right
Input
[1,3,1],
[1,5,1],
[4,2,1]
Output
7
Explanation
Because it follows the path 1→3→1→1→1, which minimizes the sum as 7.

This image shows the path followed from the top left to reach bottom right.
Algorithm for Minimum Path Sum
Now we understand the problem statement of minimum path sum. Without discussing much we just move to the algorithm used for the implementation of this problem.
- Get the input value in an array.
- Open a nested for loop and make it run until all the rows and columns traverse of the given input array.
- If i = =0 &&j = =0
- then continue, means leave this iteration and jump onto next one.
- Else if i = =0
- then array[i][j]=array[i][j]+ arr[i][j-1];
- Else if j = =0
- arr[i][j] = arr[i][j] + arr[i-1][j];
- Else
- arr[i][j] = getMin(arr[i-1][j]+arr[i][j], arr[i][j-1]+arr[i][j])
- Pass these values to getMin function which returns the minimum value between two.
- If i = =0 &&j = =0
- Return array[rows-1][columns-1];
Explanation
In minimum path sum problem, our job is to find that path in a matrix that minimizes the sum consisting of all the integers which come in the path, so we need to declare a function where the function is defined as to return the smallest value between the two values which are passed on to that function.
So now, we start a nested for loop, make the outer loop run-up to the value (row -1) is reached, and the inner loop up to column -1 is reached.
Step by Step Execution
So now let us take an example to understand minimum path sum problem,
Input : {{1,3,4},
{2,0,2},
{2,0,1}};
For now,
- i=0, j=0
If part executes and it will continue and jump onto the next one.
- i=0, j=1
else if ( i = = 0 ) executes and arr[i][j] = arr [i][j] + arr [i][j-1]
means arr[0][1]= 3+1 = 4
- i=0, j=2
else if ( i = = 0 ) executes and arr[i][j] = arr [i][j] + arr [i][j-1]
means arr[0][2]= arr[0][2] + arr [0][1] = 4 +1 =5
- i=1,j=0
else if ( j = = 0 ) executes and arr[i][j] = arr [i][j] + arr [i-1][j]
means arr[1][0]= arr[1][0] + arr [0][0] = 2 +1 =3
- i=1,j=1
else part executes and getMin( arr[i-1][j] + arr [i][j], arr [i][j-1] + arr[i][j] ) function is call
and getMin( arr[0][1]) + arr[1][1], arr[1][0]+arr[1][1]) = ( 1 + 2, 3+2)
which will return the smallest value is 3 in arr[1][1] => arr[1][1]=3
- i=1,j=2
else part executes and getMin( arr[i-1][j] + arr [i][j], arr [i][j-1] + arr[i][j] ) function is call
and getMin( arr[0][2]) + arr[1][2], arr[1][1]+arr[1][2]) = ( 5 + 2, 3+2)
which will return the smallest value is 5 in arr[1][2] => arr[1][2]=5.
arr[1][2]=5.
- i=2,j=0
else if ( j = = 0 ) executes and arr[i][j] = arr [i][j] + arr [i-1][j]
means arr[2][0]= arr[2][0] + arr [1][0] = 2 +2 =4
arr[2][2]=4.
- i=2,j=1
else part executes and getMin( arr[i-1][j] + arr [i][j], arr [i][j-1] + arr[i][j] ) function is call
and getMin( arr[1][1]) + arr[2][1], arr[2][0]+arr[2][1]) = ( 3+0, 4+0)
which will return the smallest value is 3 in arr[2][1] => arr[2][1]=3.
arr[1][2]=3.
- i=2,j=2
else part executes and getMin( arr[i-1][j] + arr [i][j], arr [i][j-1] + arr[i][j] ) function is call
and getMin( arr[1][2]) + arr[2][2], arr[2][1]+arr[2][2]) = ( 5 + 1, 3+1)
which will return the smallest value is 4 in arr[2][2] => arr[2][2]=5.
arr[2][2]=4.
And it will return the arr[2][2] which is 4 and that is our output value which defines the minimum sum path.
Output: 4
C++ Program for Minimum Path Sum
#include<iostream>
using namespace std;
int getMin(int val1, int val2)
{
return val1 < val2 ? val1 : val2;
}
int getMinimumSum(int arr[3][3])
{
for(int i=0; i<3; i++)
{
for(int j=0; j<3; j++)
{
if(i==0 && j == 0)
{
continue;
}
else if(i==0)
{
arr[i][j] = arr[i][j] + arr[i][j-1];
}
else if(j==0)
{
arr[i][j] = arr[i][j] + arr[i-1][j];
}
else
{
arr[i][j] = getMin(arr[i-1][j]+arr[i][j], arr[i][j-1]+arr[i][j]);
}
}
}
return arr[2][2];
}
int main()
{
int inputArray[3][3] = {{1,3,4},
{2,0,2},
{2,0,1}};
cout<<"Length of minimum path sum: "<<getMinimumSum(inputArray);
return 0;
}
Length of minimum path sum: 4
Java Program for Minimum Path Sum
class MinimumPathSum {
private static int getMin(int val1, int val2) {
return val1<val2 ? val1 : val2;
}
private static int getMinimumSum(int[][] arr) {
for (int i = 0; i<arr.length; i++) {
for (int j = 0; j<arr[i].length; j++) {
if (i == 0 && j == 0) {
continue;
} else if (i == 0) {
arr[i][j] = arr[i][j] + arr[i][j - 1];
} else if (j == 0) {
arr[i][j] = arr[i][j] + arr[i - 1][j];
} else {
arr[i][j] = getMin(arr[i - 1][j] + arr[i][j], arr[i][j - 1] + arr[i][j]);
}
}
}
int r = arr.length - 1;
int c = arr[0].length - 1;
return arr[r][c];
}
public static void main(String[] args) {
int[][] inputArray = {{1, 3, 4},
{2, 0, 2},
{2, 0, 1}};
System.out.println("Length of minimum path sum: " + getMinimumSum(inputArray));
}
}Length of minimum path sum: 4
Complexity Analysis for Minimum Path Sum
Time Complexity
O(m*n) where “m” and “n” are the numbers of rows and columns in the matrix given in the minimum path sum problem.
Space Complexity
O(1) because we don’t use any auxiliary space while implement the approach for minimum path sum.