In the sudoku solver problem we have given a partially filled (9 x 9) sudoku, write a program to complete the puzzle.
Sudoku must satisfy the following properties,
- Every number(1-9) must appear exactly once in a row and once in a column.
- Every number(1-9) must appear exactly once in a (3 x 3) sub-box of the grid.
0 represents an empty cell.
Table of Contents
Example
Input:

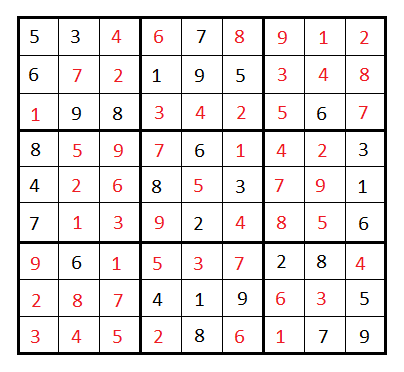
Output:
Algorithm
The basic algorithm to solve the sudoku puzzle(sudoku solver) is to try all the combinations of the numbers and choose the solution that satisfies the above conditions.
The time complexity of this process is very high, so we use backtracking to cut down the recursion as soon as we found that the current path will not lead to a solution.
This tends to reduce the time taken to solve the puzzle, but the overall upper bound on time complexity remains the same.
- Find an empty cell, if there is no empty cell, then the puzzle is solved and we return.
- Let the row and column of the empty cell be i and j respectively.
- Assign numbers one by one to the empty cell, if it is safe to assign a number, recursively repeat the above steps.
- If this assignment leads to a solution, return true.
- Else try the next number for the current empty cell.
Checking if the assignment is safe or not,
For a number to be valid in a cell, it should follow the basic properties of the sudoku puzzle(described above).
- If the assigned number exists in the current row or current column, return false.
- Calculate the starting index of row and column of the 3×3 sub box in which the empty cell is present.
- If the assigned number exists in the current 3×3 sub box, return false.
- Return true.
Pseudo Code for Sudoku Solver
// Function to solve the sudoku puzzle
solve(sudoku)
// Find an empty cell
int i = 0, j = 0
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (sudoku[i][j] == 0)
break
}
}
// No empty cell found
if (i == 9 && j == 9)
return true
// Try all the numbers one by one
for (int n = 1; n <= 9; n++) {
// If the assignment is valid
if (isSafe(sudoku, i, j, n)) {
// Assign the value to this cell
sudoku[i][j] = n
// If recursion leads to a solution, return true
if (solve(sudoku))
return true
// Back tracking
sudoku[i][j] = 0
}
}// Function to check the validity of a number at a given cell
isSafe(sudoku, i, j, n)
// Check in current row and column
for (int x = 0; x < 9; x++)
if (sudoku[i][x] == n || sudoku[x][j] == n)
return false
// Calculate starting index of row and column of 3 x 3 sub box
int rs = i - (i % 3)
int cs = j - (j % 3)
// Check in 3 x 3 sub box
for (int x = 0; x < 3; x++)
for (int y = 0; y < 3; y++)
if (sudoku[x + rs][y + cs] == n)
return false
return trueJAVA Code
public class SudokoSolver {
public static boolean solve(int[][] sudoku) {
int i = 0, j = 0;
boolean found = false;
// Find an empty cell
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if (sudoku[i][j] == 0) {
found = true;
break;
}
}
if (found) {
break;
}
}
// No empty cell found, return true
if (i == 9 && j == 9) {
return true;
}
// One by one try all the values in the current cell
for (int n = 1; n <= 9; n++) {
// check if it is valid to assign value n to current cell
if (isSafe(i, j, n, sudoku)) {
sudoku[i][j] = n;
// Recursively solve the sudoku
if (solve(sudoku)) {
return true;
}
// back track if the recursion returns false
sudoku[i][j] = 0;
}
}
// Return false if no value fits
return false;
}
public static boolean isSafe(int i, int j, int n, int[][] sudoku) {
// Check in current row and column
for (int x = 0; x < 9; x++) {
// Row
if (sudoku[i][x] == n) {
return false;
}
// Column
if (sudoku[x][j] == n) {
return false;
}
}
// Calculate the starting index of row and column of current 3x3 sub box
int rs = i - (i % 3);
int cs = j - (j % 3);
// Check in the current sub box
for (int x = 0; x < 3; x++) {
for (int y = 0; y < 3; y++) {
if (sudoku[x + rs][y + cs] == n) {
return false;
}
}
}
// Return true
return true;
}
public static void main(String[] args) {
// Partially filled sudoku puzzle
int[][] sudoko = new int[][] {
{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}
};
solve(sudoko);
// Print the answer
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
System.out.print(sudoko[i][j] + " ");
}
System.out.println();
}
}
}C++ Code for Sudoku Solver
#include <bits/stdc++.h>
using namespace std;
bool isSafe(vector<vector<int>> &sudoku, int i, int j, int n) {
// Check in current row and column
for (int x = 0; x < 9; x++) {
// Row
if (sudoku[i][x] == n) {
return false;
}
// Column
if (sudoku[x][j] == n) {
return false;
}
}
// Calculate the starting index of row and column of current 3x3 sub box
int rs = i - (i % 3);
int cs = j - (j % 3);
// Check in the current sub box
for (int x = 0; x < 3; x++) {
for (int y = 0; y < 3; y++) {
if (sudoku[x + rs][y + cs] == n) {
return false;
}
}
}
// Return true
return true;
}
bool solve(vector<vector<int>> &sudoku) {
int i = 0, j = 0;
bool found = false;
// Find an empty cell
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if (sudoku[i][j] == 0) {
found = true;
break;
}
}
if (found)
break;
}
// No empty cell found, return true
if (i == 9 && j == 9) {
return true;
}
// One by one try all the values in the current cell
for (int n = 1; n <= 9; n++) {
// check if it is valid to assign value n to current cell
if (isSafe(sudoku, i, j, n)) {
sudoku[i][j] = n;
// Recursively solve the sudoku
if (solve(sudoku) == true)
return true;
// back track if the recursion returns false
sudoku[i][j] = 0;
}
}
// Return false if no value fits
return false;
}
int main() {
// Partially filled sudoku puzzle
vector<vector<int>> sudoku = {
{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}
};
solve(sudoku);
// Print the answer
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
cout<<sudoku[i][j]<<" ";
}
cout<<endl;
}
return 0;
}5 3 4 6 7 8 9 1 2 6 7 2 1 9 5 3 4 8 1 9 8 3 4 2 5 6 7 8 5 9 7 6 1 4 2 3 4 2 6 8 5 3 7 9 1 7 1 3 9 2 4 8 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 5 2 8 6 1 7 9
Complexity Analysis for Sudoku Solver
Time Complexity
O(9^(n*n)): For every unassigned index there are 9 possible options so the worst-case time complexity of sudoku solver is O(9^(n*n)).
Space Complexity
O(n*n): To store the output array a matrix is needed.