Suppose a man standing in the first cell or the top left corner of “a × b” matrix. A man can move only either up or down. That person wants to reach his destination and that destination for him is the last cell of the matrix or bottom right corner.
And if there are some hurdles in it, how many unique paths can be identified by the person. Help him to reach the destination by knowing No of Unique Paths.
A hurdle is considered as 1 and space is marked as 0 in the matrix.
Table of Contents
Example
Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output:
2
Explanation:
Because only one hurdle is present in the middle of the whole matrix which allows only two unique paths:-
- Down →Down →Right →Right
- Right →Right →Down →Down
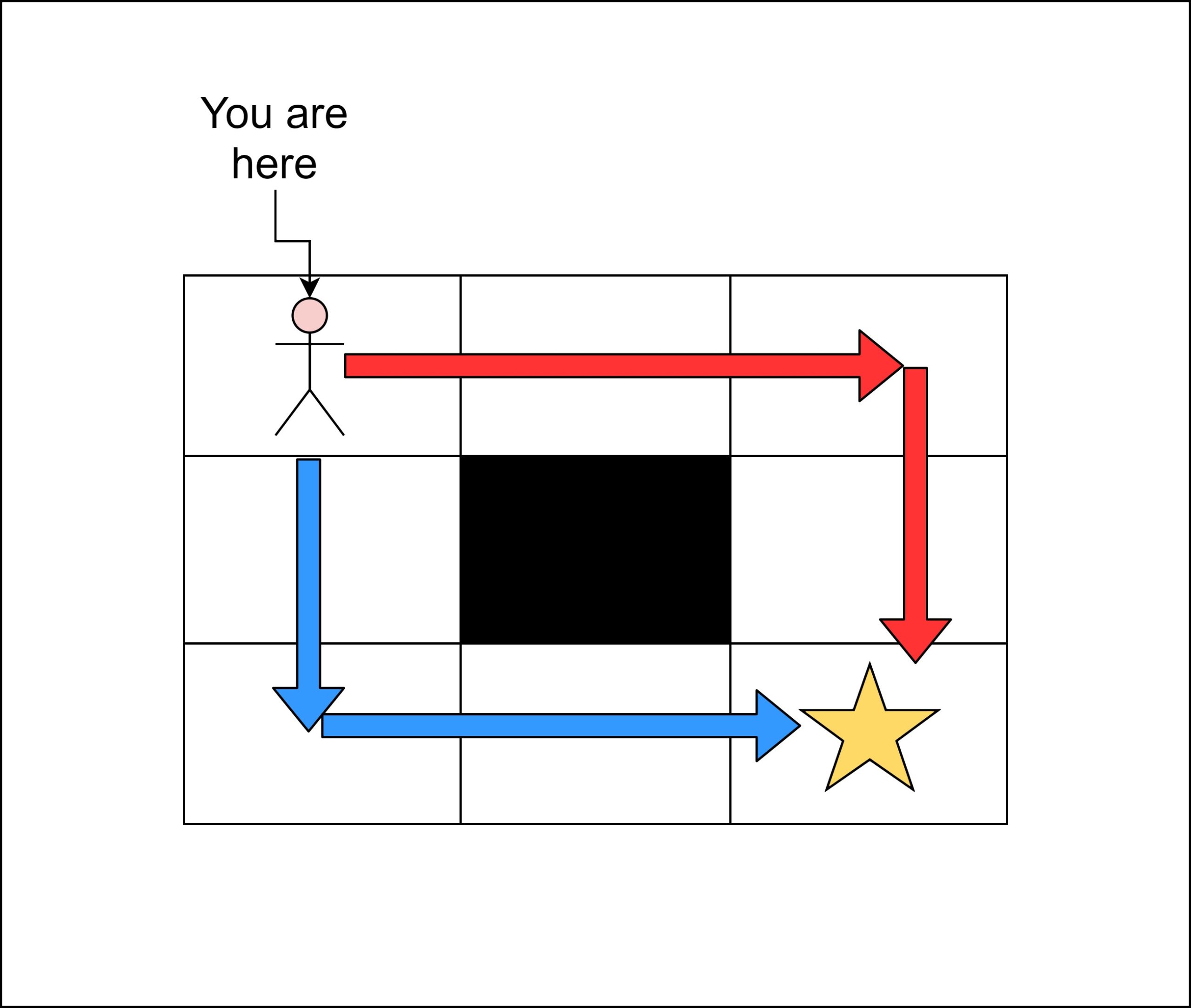
In the above image, the blue arrow shows path 1 and the red arrow shows path 2.
Algorithm
- Check if the first cell that is array[0][0] contains 1 then return the unique paths as 0 as it can’t move forward than this.
- If array[0][0] doesn’t contain the value 1 then initialize the value of array[0][0]=1.
- Now, iterate over the first row of the array and if this cell contains 1, this means the current cell has a hurdle in it and sets the value of a cell to 0. Else set the value of this cell as of the previous cell that is array[i][j]= array[i][j-1].
- Now, iterate over the first column of the array and if this cell contains 1, this means the current cell has a hurdle in it and sets the value of the cell to 0. Else set the value of this cell as of the previous cell that is array[i][j]= array[i][j-1].
- Now, iterate over the whole matrix starting from the cell array[1][1].
- Check if cell doesn’t contain any hurdle then do arrayi,j] = array [i-1,j] + array [i,j-1].
- If a cell contains a hurdle, then set the value of the cell to 0 to make sure it doesn’t repeat in any other path.
Explanation
So our main idea for solving this question is if a cell doesn’t have the values 0 in it then it means that we have the number of ways of reaching our destination cell is the sum of a number of ways of reaching the cell above that cell and sum of the number of ways of reaching the cell left of that cell.
So we implemented some of the functions which are going to help us in solving our problem. We declared a function getVal, getVal gets some arguments perform some operations and return some value, that is going to solve the following problem:
- If in a first row, a cell contains a hurdle it sets the value to 0 else it will set the value of that cell as that of the previous cell that is array[i][j]=array[i][j-1].
- If in a first row, a cell contains a hurdle it sets the value to 0 else it will set the value of that cell as that of the previous cell that is array[i][j]=array[i-1][j].
Example
So let us take an example as Array={{0,0,0},{0,1,0},{0,0,0}};
An array is passed into findUniquePath
Array={{0,0,0},{0,1,0},{0,0,0}};
So its first cell that is array[0][0] is not equal to 1.
So set, array[0][0]=1;
Iterating over column,
i=1
if array[1][0]==0 and array[0][0]=1 is true
so array[1][0]=1;
i=2;
if array[2][0]==0 and array[1][0]=1 is true
so array[2][0]=1;
Now iterating over row,
i=1
if array[0][1]==0 and array[0][0]=1 is true
so array[0][1]=1;
i=2;
if array[0][2]==0 and array[0][1]=1 is true
so array[0][2]=1;
Now starting from array[1][1]
i=1,j=1
if array[1][1]==0 is false
so array[1][1]=0
i=1,j=2
if array[1][2]==0 is true
array[i][j] = array[i – 1][j] + array[i][j – 1];
so array[1][2]=array[0][2]+array[0][1];
array[1][2]=1+1=2;
i=2,j=1
if array[2][1]==0 is true
so array[2][1]=0
i=2,j=2
if array[2][2]==0 is true
array[i][j] = array[i – 1][j] + array[i][j – 1];
so array[2][2]=array[1][2]+array[2][1];
array[2][2]=2+0;
array[2][2]=2
That is we are going to return the value array[2][2] which means 2 is our required output.
Implementation
C++ program for Unique Paths II
#include<iostream>
using namespace std;
int getVal(int x, int y)
{
if(x==0 && y==1)
{
return 1;
}
else
{
return 0;
}
}
int findUniquePath(int arr[3][3])
{
if (arr[0][0] == 1)
{
return 0;
}
arr[0][0] = 1;
for (int i = 1; i < 3; i++)
{
arr[i][0] = getVal(arr[i][0],arr[i-1][0]);
}
for (int i = 1; i < 3; i++)
{
arr[0][i] = getVal(arr[0][i],arr[0][i-1]);
}
for (int i = 1; i < 3; i++)
{
for (int j = 1; j < 3; j++)
{
if (arr[i][j] == 0)
{
arr[i][j] = arr[i - 1][j] + arr[i][j - 1];
}
else
{
arr[i][j] = 0;
}
}
}
return arr[2][2];
}
int main()
{
int inputValue[3][3]= {{0,0,0},
{0,1,0},
{0,0,0}};
findUniquePath(inputValue);
cout<<findUniquePath(inputValue);;
return 0;
}
2
Java program for Unique Paths II
class uniquePath2 {
public static int getVal(int x, int y) {
if (x == 0 && y == 1) {
return 1;
} else {
return 0;
}
}
public static int findUniquePath(int array[][]) {
if (array[0][0] == 1) {
return 0;
}
array[0][0] = 1;
for (int i = 1; i<array.length; i++) {
array[i][0] = getVal(array[i][0], array[i - 1][0]);
}
for (int i = 1; i<array[0].length; i++) {
array[0][i] = getVal(array[0][i], array[0][i - 1]);
}
for (int i = 1; i<array.length; i++) {
for (int j = 1; j<array[i].length; j++) {
if (array[i][j] == 0) {
array[i][j] = array[i - 1][j] + array[i][j - 1];
} else {
array[i][j] = 0;
}
}
}
int row = array.length;
int col = array[0].length;
return array[row - 1][col - 1];
}
public static void main(String[] args) {
int inputValue[][] = {
{
0, 0, 0
}, {
0, 1, 0
}, {
0, 0, 0
}
};
System.out.println(findUniquePath(inputValue));
}
}2
Complexity Analysis for Unique Paths II
Time Complexity
O(a × b) where a and b is the number of rows and columns in the matrix given to us as each cell is processed only once.
Space Complexity
O(1) as no extra space is being utilized since we are using dynamic programming.