Table of Contents
Problem Statement
The problem “Find the First Circular Tour that visits all the Petrol Pumps” states that there are N petrol pumps on a circular road. Given the petrol that every petrol pump has and the amount of petrol required to cover the distance between two petrol pumps. So you need to find the first petrol pump where a truck starts and can complete the circle.
The input format is as, {x, y}, where x is the petrol that the petrol pump has and y is the fuel needed to reach from this petrol pump to next petrol pump.
If there is no possible tour, output -1.
Examples
{{5, 3}, {2, 7}, {11, 2}, {8, 9}}3
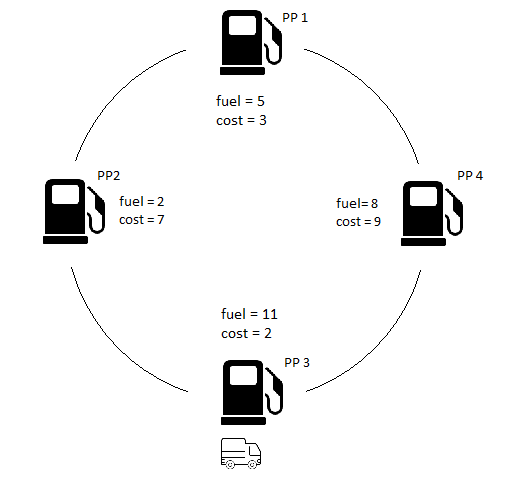
{{1, 1}, {2, 2}, {1, 2}, {3, 1}}4
{{2, 3}, {4, 5}, {1, 1}, {3, 3}}-1
Naive Approach
One by one consider every petrol pump as starting point. If there exists a possibly valid tour. Return the current petrol pump number. Else if there is no possible tour from any petrol pump, return -1.
- Run a loop from 1 to n, this loop consider the ith petrol pump as the starting point.
- Initialize a variable currFuel as 0, which represents the amount of petrol in the truck.
- To travel from jth petrol pump to (j + 1)th petrol pump, (fuel[j] – cost[j]) amount of fuel is added to currFuel.
- From the ith petrol pump start traveling ahead in the circle and add the extra fuel(fuel[j] – cost[j]) at every step, repeat this process while currFuel >= 0.
- If the truck is able to traverse through all the n petrol pumps, return i. Else continue for next i.
- If there is no i for which the truck can traverse the whole circle, return -1.
Code
JAVA Code to Find the First Circular Tour that visits all the Petrol Pumps
class FindTheFirstCircularTourThatVisitsAllThePetrolPumps {
private static int findPetrolPump(int[] fuel, int[] costs) {
// Total number of petrol pumps
int n = fuel.length;
// one by one consider all the petrol pumps as starting point
for (int i = 0; i < n; i++) {
// initialize currPetrol as 0, it represents the amount of petrol in the truck
int currPetrol = 0;
// travelled represents the number of petrol pumps travelled by truck
int travelled = 0;
// while there is some petrol in the truck, travel to the next petrol pump
while (currPetrol >= 0 && travelled < n) {
// fuel added to the truck when it cross petrol pump
// number j is (fuel[j] - cost[j])
currPetrol += (fuel[(i + travelled) % n] - costs[(i + travelled) % n]);
travelled++;
}
// if the truck has travelled all the petrol pumps
// with some fuel left, return i
if (travelled == n && currPetrol >= 0) {
return (i + 1);
}
}
// no possible way to travel the circle
return -1;
}
public static void main(String[] args) {
// Example 1
int fuel1[] = new int[] {5, 2, 11, 8};
int costs1[] = new int[] {3, 7, 2, 9};
System.out.println(findPetrolPump(fuel1,costs1));
// Example 2
int fuel2[] = new int[] {1, 2, 1, 3};
int costs2[] = new int[] {1, 2, 2, 1};
System.out.println(findPetrolPump(fuel2, costs2));
// Example 3
int fuel3[] = new int[] {2, 4, 1, 3};
int costs3[] = new int[] {3, 5, 1, 3};
System.out.println(findPetrolPump(fuel3, costs3));
}
}3 4 -1
C++ Code to Find the First Circular Tour that visits all the Petrol Pumps
#include <iostream>
using namespace std;
int findPetrolPump(int *fuel, int *costs, int n) {
// one by one consider all the petrol pumps as starting point
for (int i = 0; i < n; i++) {
// initialize currPetrol as 0, it represents the amount of petrol in the truck
int currPetrol = 0;
// travelled represents the number of petrol pumps travelled by truck
int travelled = 0;
// while there is some petrol in the truck, travel to the next petrol pump
while (currPetrol >= 0 && travelled < n) {
// fuel added to the truck when it cross petrol pump
// number j is (fuel[j] - cost[j])
currPetrol += (fuel[(i + travelled) % n] - costs[(i + travelled) % n]);
travelled++;
}
// if the truck has travelled all the petrol pumps
// with some fuel left, return i
if (travelled == n && currPetrol >= 0) {
return (i + 1);
}
}
// no possible way to travel the circle
return -1;
}
int main() {
// Example 1
int fuel1[] = {5, 2, 11, 8};
int costs1[] = {3, 7, 2, 9};
cout<<findPetrolPump(fuel1, costs1, sizeof(fuel1) / sizeof(fuel1[0]))<<endl;
// Example 2
int fuel2[] = {1, 2, 1, 3};
int costs2[] = {1, 2, 2, 1};
cout<<findPetrolPump(fuel2, costs2, sizeof(fuel2) / sizeof(fuel2[0]))<<endl;
// Example 3
int fuel3[] = {2, 4, 1, 3};
int costs3[] = {3, 5, 1, 3};
cout<<findPetrolPump(fuel3, costs3, sizeof(fuel3) / sizeof(fuel3[0]))<<endl;
return 0;
}3 4 -1
Complexity Analysis
Time Complexity
O(n2), is the time complexity. Where N is the number of petrol pumps in the given input. Here we have polynomial complexity because we have considered each petrol pump as starting point. After making each petrol pump as starting we made a complete tour. And checked whether during the tour the petrol tank gets empty. So we had N starting points and then each starting point had N-1 petrol pumps to cover. Thus the time complexity is O(N^2).
Space Complexity
O(1), here we haven’t saved any information which was required for each element simultaneously. And thus we have not used much space. We have used a constant number of variables which made the space complexity constant.
Optimal Approach
The optimal idea is to solve this problem is to use a queue. Initialize a variable currFuel as 0. Keep on pushing petrol pumps to queue while currFuel >= 0, and after pushing a petrol pump to queue currFuel is incremented by (fuel[i] – cost[i]). If at any moment currFuel becomes negative, pop out petrol pumps from queue one by one till currFuel is negative. If all the n petrol pumps are present in queue, return the starting point, else if there is no way that n petrol pumps can be in the queue, return -1.
The space used by queue can be saved if we form a queue in the fuel and cost array itself. It can be achieved by using start and end pointers on the arrays.
- Initialize start, end and currFuel as 0, where start represents the starting point of the truck, end represents the next petrol pump to visit and currFuel represents the amount of fuel in the truck.
- Push the first petrol pump into queue and increment currFuel by (fuel[0] – cost[0]) and increment end.
- Repeat the next steps till either all the petrol pumps are not added to queue or it is found that there is no solution.
- If the value of currFuel becomes negative, pop out petrol pump at position start from queue and decrement currFuel by (fuel[start] – cost[start]) and increment start. If start becomes 0, there is no possible solution, return -1.
- Else add the petrol pump at position end to the queue, increment currFuel by (fuel[end] – cost[end]), and increment end.
- If all the petrol pumps are present in queue, that is, end is equals to start, return start.
Code
JAVA Code to Find the First Circular Tour that visits all the Petrol Pumps
class FindTheFirstCircularTourThatVisitsAllThePetrolPumps {
private static int findPetrolPump(int[] fuel, int[] costs) {
// total number of petrol pumps
int n = fuel.length;
// initialize start and end as 0
int start = 0, end = 0;
// initialize currFuel as 0
int currFuel = 0;
// push the first petrol pump to queue
currFuel += (fuel[end] - costs[end]);
// increment end
end = (end + 1) % n;
while (end != start || currFuel < 0) {
// if currFuel becomes negative, one by one pop out
// petrol pumps from queue
while (currFuel < 0) {
currFuel -= (fuel[start] - costs[start]);
start = (start + 1) % n;
// if start again becomes 0, there is no possible solution
if (start == 0) {
return -1;
}
}
// Push the current petrol pump to queue and update currFuel
currFuel += (fuel[end] - costs[end]);
end = (end + 1) % n;
}
// return the start point
return (start + 1);
}
public static void main(String[] args) {
// Example 1
int fuel1[] = new int[] {5, 2, 11, 8};
int costs1[] = new int[] {3, 7, 2, 9};
System.out.println(findPetrolPump(fuel1,costs1));
// Example 2
int fuel2[] = new int[] {1, 2, 1, 3};
int costs2[] = new int[] {1, 2, 2, 1};
System.out.println(findPetrolPump(fuel2, costs2));
// Example 3
int fuel3[] = new int[] {2, 4, 1, 3};
int costs3[] = new int[] {3, 5, 1, 3};
System.out.println(findPetrolPump(fuel3, costs3));
}
}3 4 -1
C++ Code to Find the First Circular Tour that visits all the Petrol Pumps
#include <iostream>
using namespace std;
int findPetrolPump(int *fuel, int *costs, int n) {
// initialize start and end as 0
int start = 0, end = 0;
// initialize currFuel as 0
int currFuel = 0;
// push the first petrol pump to queue
currFuel += (fuel[end] - costs[end]);
// increment end
end = (end + 1) % n;
while(end != start || currFuel < 0) {
// if currFuel becomes negative, one by one pop out
// petrol pumps from queue
while (currFuel < 0) {
currFuel -= (fuel[start] - costs[start]);
start = (start + 1) % n;
// if start again becomes 0, there is no possible solution
if (start == 0) {
return -1;
}
}
// Push the current petrol pump to queue and update currFuel
currFuel += (fuel[end] - costs[end]);
end = (end + 1) % n;
}
// return the start point
return (start + 1);
}
int main() {
// Example 1
int fuel1[] = {5, 2, 11, 8};
int costs1[] = {3, 7, 2, 9};
cout<<findPetrolPump(fuel1, costs1, sizeof(fuel1) / sizeof(fuel1[0]))<<endl;
// Example 2
int fuel2[] = {1, 2, 1, 3};
int costs2[] = {1, 2, 2, 1};
cout<<findPetrolPump(fuel2, costs2, sizeof(fuel2) / sizeof(fuel2[0]))<<endl;
// Example 3
int fuel3[] = {2, 4, 1, 3};
int costs3[] = {3, 5, 1, 3};
cout<<findPetrolPump(fuel3, costs3, sizeof(fuel3) / sizeof(fuel3[0]))<<endl;
return 0;
}3 4 -1
Complexity Analysis
Time Complexity
O(n), using queue has saved us time and we are able to solve the problem in linear time.
Space Complexity
O(1), we were using a queue and that would have cost us linear space complexity. But instead of that,we used pointers to use the initial input arrays as queues. And thus saving us space.