Priority Queue

A priority queue is a type of data structure which is similar to a regular queue but has a priority associated with each of its element. Higher the priority earlier the element will be served. In some cases, there are two elements with the same priority then, the element enqueued first will be served first.

Example

Suppose there are 2 jobs namely, A and B where job A has higher priority than job B. Let the scheduling of job be in the following order:

1. A
2. B
3. A

In the following order priority queue will be formed:

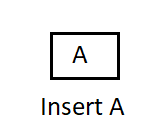
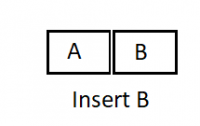
So here you see that jobs with higher priority are assigned before the jobs with lower priority.

Types of Priority Queue

1. Ascending order priority queue

   In this type of priority_queue, a lower priority number is assigned to jobs of higher priority.
   For example: If two jobs namely A and B are assigned numbers 1 and 2, where job A is of higher priority, then A will be assigned 1, and job B will be assigned 2.

2. Descending order priority queue

   In this type of priority_queue, jobs with higher priority are assigned a higher priority number.
   For example: If two jobs namely A and B are assigned numbers 1 and 2, where job A is of higher priority, then A will be assigned 2, and job B will be assigned 1.

Operation performed by Priority Queue

The basic operations performed by a priority_queue are as follows:

1. Insertion: Insert an item in the queue according to its priority.
2. Delete: Removes an item from the queue.
3. getHighestPriority: Gives you the highest priority element.

Priority_queue supports a few more operations:

1. Peek: Get the element at front of the queue.
2. isFull: checks if the queue is full.
3. isEmpty: checks if the queue is empty.

Applications

1. In scheduling like CPU scheduling, Disk Scheduling, etc.
2. Graph Algorithms ( Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc)

Implementation

Priority queue can be implemented using various data structures like an array, linked list, etc. Some of the data structures are given below with their time complexities:

1. Arrays (O(n * log(n)))
2. Linked List (O(n)
3. Heap (O(log(n)))

Out of all the data structure heap data structure provides the best time complexity while implementing a priority_queue.

References