Reversing a Queue using Recursion

In reversing a queue using recursion problem we have given a queue, write a recursive algorithm to reverse the queue using recursion.

Examples

Input
10 -> 9 -> 3 -> 11 -> 5
Output
5 -> 11 -> 3 -> 9 -> 10

Input
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8
Output
8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1

Algorithm for Reversing a Queue using Recursion

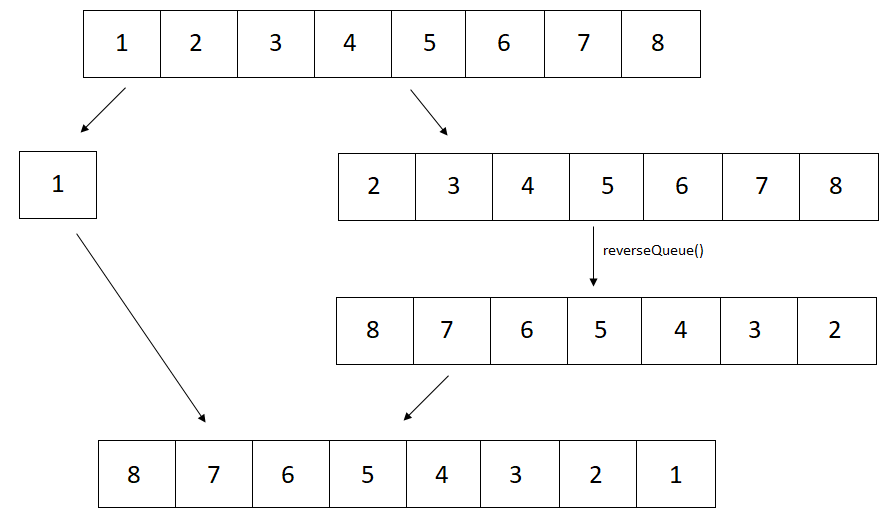
Let us imagine that the function reverse(queue) is a recursive function that reverses the queue given to it. Its definition can be understood by an example,

queue = 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8
reverse(1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8) = reverse(2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8) -> 1
reverse(2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8) = reverse(3 -> 4 -> 5 -> 6 -> 7 -> 8) -> 2
reverse(3 -> 4 -> 5 -> 6 -> 7 -> 8) = reverse(4 -> 5 -> 6 -> 7 -> 8) -> 3
reverse(4 -> 5 -> 6 -> 7 -> 8) = reverse(5 -> 6 -> 7 -> 8) -> 4
reverse(5 -> 6 -> 7 -> 8) = reverse(6 -> 7 -> 8) -> 5
reverse(6 -> 7 -> 8) = reverse(7 -> 8) -> 6
reverse(7 -> 8) = reverse(8) -> 7
reverse(8) = reverse() -> 8
reverse() = empty queue

So,
reverse(8) = 8
reverse(7 -> 8) = 8 -> 7
reverse(6 -> 7 -> 8) = 8 -> 7 -> 6
reverse(5 -> 6 -> 7 -> 8) = 8 -> 7 -> 6 -> 5
reverse(4 -> 5 -> 6 -> 7 -> 8) = 8 -> 7 -> 6 -> 5 -> 4
reverse(3 -> 4 -> 5 -> 6 -> 7 -> 8) = 8 -> 7 -> 6 -> 5 -> 4 -> 3
reverse(2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8) = 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2
reverse(1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8) = 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1

Base Case of recursion: The reverse of an empty queue is an empty queue.

1. If the queue is empty, return, else pop out the first element of the queue and store it in a variable, say curr.
2. Call the reverse method recursively on the remaining queue.
3. The reverse method will reverse the remaining queue, push the curr element to the queue.
4. The queue is reversed, prints its elements.

JAVA Code for Reversing a Queue using Recursion

import java.util.LinkedList;
import java.util.Queue;

public class ReversingAQueueUsingRecursion {
    private static void reverseQueue(Queue<Integer> queue) {
        // Base case
        // reverse of an empty queue is an empty queue
        if (queue.isEmpty()) {
            return;
        }

        // remove an element from queue and store it in a variable, say curr
        int curr = queue.poll();
        // recursively call the reverseQueue method on remaining queue
        reverseQueue(queue);
        // add the removed element to the end of the reversed queue
        queue.add(curr);
    }

    public static void main(String[] args) {
        // Example 1
        Queue<Integer> q1 = new LinkedList<>();
        q1.add(10);
        q1.add(9);
        q1.add(3);
        q1.add(11);
        q1.add(5);
        reverseQueue(q1);
        for (Integer i : q1) {
            System.out.print(i + " ");
        }
        System.out.println();

        // Example 2
        Queue<Integer> q2 = new LinkedList<>();
        q2.add(1);
        q2.add(2);
        q2.add(3);
        q2.add(4);
        q2.add(5);
        q2.add(6);
        q2.add(7);
        q2.add(8);
        reverseQueue(q2);
        for (Integer i : q2) {
            System.out.print(i + " ");
        }
        System.out.println();
    }
}

5 11 3 9 10 
8 7 6 5 4 3 2 1

C++ Code for Reversing a Queue using Recursion

#include<bits/stdc++.h> 
using namespace std; 

void reverseQueue(queue<int> &q) {
    // Base case
    // reverse of an empty queue is an empty queue
    if (q.empty()) {
        return;
    }
    
    // remove an element from queue and store it in a variable, say curr
    int curr = q.front();
    q.pop();
    // recursively call the reverseQueue method on remaining queue
    reverseQueue(q);
    // add the removed element to the end of the reversed queue
    q.push(curr);
}

int main() {
    // Example 1
    queue<int> q1;
    q1.push(10);
    q1.push(9);
    q1.push(3);
    q1.push(11);
    q1.push(5);
    reverseQueue(q1);
    while (!q1.empty()) {
        cout<<q1.front()<<" ";
        q1.pop();
    }
    cout<<endl;
    
    // Example 2
    queue<int> q2;
    q2.push(1);
    q2.push(2);
    q2.push(3);
    q2.push(4);
    q2.push(5);
    q2.push(6);
    q2.push(7);
    q2.push(8);
    reverseQueue(q2);
    while (!q2.empty()) {
        cout<<q2.front()<<" ";
        q2.pop();
    }
    cout<<endl;
    
    return 0;
}

5 11 3 9 10 
8 7 6 5 4 3 2 1

Complexity Analysis

Time Complexity = O(n)
Space Complexity = O(n), due to recursion which uses the stack concept.
where n is the number of elements in the queue.

References