Smallest Multiple of a Given Number

In the smallest multiple of a given number made of digits 0 and 9 only problem we have given a number n, find the smallest number made from digits 0 and 9 that is divisible by n. Assume that the answer will not exceed 10⁶.

Examples

Input
3
Output
9

Input
5
Output
90

Input
4
Output
900

Algorithm for Smallest Multiple of a Given Number

Generating all the numbers formed using only 9 and 0 is similar to producing binary numbers. That is the numbers containing only 9 and 0 can be viewed as a tree, with root as 9 and for every node the left child is obtained by appending ‘0’ to it and right child is obtained by appending ‘9’ to it.

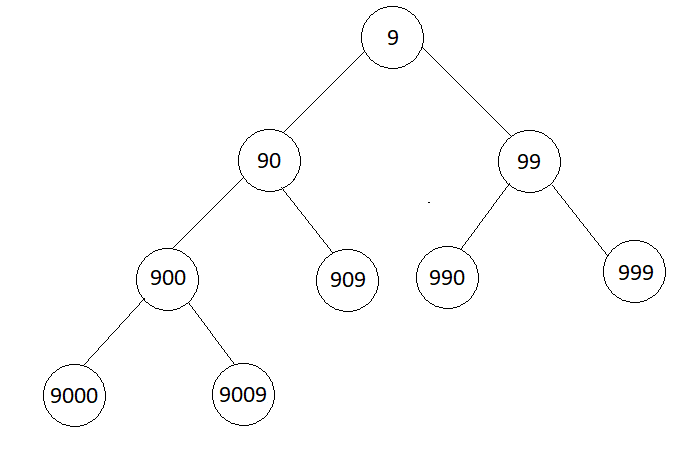
The idea is to generate some numbers using the level order traversal in above tree and store them in a list before processing any input. For a given number n, traverse in the list formed and return the first number divisible by n.

1. Create a list of string that will store the numbers made up of 9 and 0.
2. Create a queue of string and push “9” to it, that is, the root of the tree.
3. Run a loop from 0 to 100, as we will push first 100 nodes of the tree to the list.
4. In every iteration, remove an element from queue, push it to the list, add its left child(element + “0”) and right child(element + “9”) to the queue.
5. For a given value of n, traverse in the list formed above, and return the first number divisible by n.

In the above algorithm, we build the tree containing elements made with 0 and 9, of 100 nodes, so in this algorithm the value of maxNodes is 100.

JAVA Code for Smallest Multiple of a Given Number

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class SmallestMultipleOfAGivenNumberMadeOfDigits0And9Only {
    private static ArrayList<String> numbers = new ArrayList<>();
    private static int MAX = 100;

    private static void generateNumbers() {
        // Create a queue for level order traversal of the tree
        Queue<String> q = new LinkedList<>();
        // push the root to the queue
        q.add("9");

        // add the first MAX nodes of tree to list numbers
        for (int i = 0; i < MAX; i++) {
            // remove an element from queue
            String curr = q.poll();
            // push it to the list
            numbers.add(curr);
            // add its children to the queue
            q.add(curr + "0");
            q.add(curr + "9");
        }
    }

    private static int firstMultiple(int n) {
        try {
            // traverse in the list and return the first number divisible by n
            for (int i = 0; i < numbers.size(); i++) {
                int curr = Integer.parseInt(numbers.get(i));
                if (curr % n == 0) {
                    return curr;
                }
            }
        } catch (Exception e) {
            e.printStackTrace();
        }
        return 0;
    }

    public static void main(String[] args) {
        // pre computation
        generateNumbers();

        // Example 1
        int n1 = 3;
        System.out.println(firstMultiple(n1));

        // Example 2
        int n2 = 5;
        System.out.println(firstMultiple(n2));

        // Example 3
        int n3 = 4;
        System.out.println(firstMultiple(n3));
    }
}

9
90
900

C++ Code for Smallest Multiple of a Given Number

#include <bits/stdc++.h> 
using namespace std; 

int MAX = 100;
vector<std::string> numbers;

void generateNumbers() {
    // Create a queue for level order traversal of the tree
    queue<std::string> q;
    // push the root to the queue
    q.push("9");
    
    // add the first MAX nodes of tree to list numbers
    for (int i = 0; i < MAX; i++) {
        // remove an element from queue
        string curr = q.front();
        q.pop();
        // push it to the list
        numbers.push_back(curr);
        // add its children to the queue
        q.push(curr + "0");
        q.push(curr + "9");
    }
}

int firstMultiple(int n) {
    // traverse in the list and return the first number divisible by n
    for (int i = 0; i < numbers.size(); i++) {
        int curr = stoi(numbers[i]);
        if (curr % n == 0) {
            return curr;
        }
    }
    return 0;
}

int main() {
    // pre computation
    generateNumbers();

    // Example 1
    int n1 = 3;
    cout<<firstMultiple(n1)<<endl;

    // Example 2
    int n2 = 5;
    cout<<firstMultiple(n2)<<endl;

    // Example 3
    int n3 = 4;
    cout<<firstMultiple(n3)<<endl;
    
    return 0;
}

9
90
900

Complexity Analysis

Time Complexity = O(maxNodes)
Space Complexity = O(maxNodes)
where maxNodes is the number of maximum nodes we build the tree with.

References