Find Maximum Sum Possible Equal Sum of Three Stacks

Difficulty Level Medium
Frequently asked in Amazon Fanatics Fourkites
StackViews 2325

Given 3 arrays stack1[ ], stack2[ ] and stack3[ ] representing stacks and the starting index of these arrays are treated as their top. Find the common maximum sum possible in all the three stacks i.e. the sum of elements of stack1, stack2 and stack3 are equal. Removal of the top is allowed in each array to find the common maximum sum.

Find Maximum Sum Possible Equal Sum of Three Stacks

Example

Input 

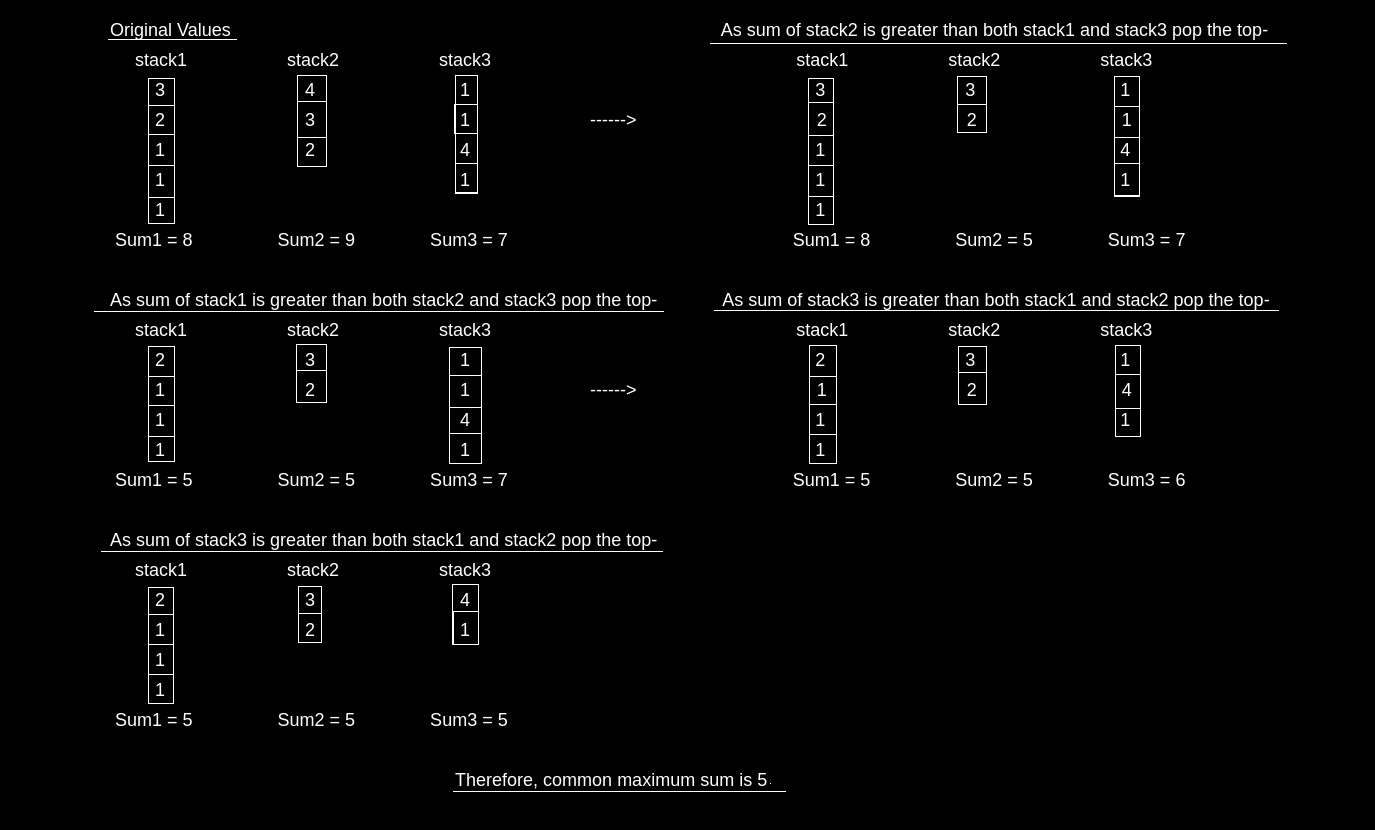
stack1[ ] = {3, 2, 1, 1, 1}
stack2[ ] = {4, 3, 2}
stack3[ ] = {1, 1, 4, 1}

Output:   5

Input 

stack1[ ] = {3, 10}
stack2[ ] = {4, 5}
stack3[ ] = {2, 1}

Output:   0

Algorithm

Now we know the problem statement of Find Maximum Sum Possible Equal Sum of Three Stacks. So, now quickly read the algorithm used for its implementation.

  1. Initialize 3 arrays representing stacks.
  2. Calculate the sum of elements of all three arrays individually. Also, declare 3 variables to store top i.e. first element of all the arrays as 0.
  3. While true check if the top of an array is equal to its size, return 0.
  4. Else if the individual sum of all the arrays is equal, return the sum.
  5. If the sum of the first array is greater than or equal to the individual sum of second array and third array, subtract the top element of the first array from its sum and increment the top variable of the first array.
  6. Else if the sum of the second array is greater than or equal to the individual sum of the first array and third array, subtract the top element of the second array from its sum and increment the top variable of the second array.
  7. Else if the sum of the third array is greater than or equal to the individual sum of first array and second array, subtract the top element of the third array from its sum and increment the top variable of the third array.

C++ Program to find maximum sum possible equal sum of three stacks

#include<bits/stdc++.h> 
using namespace std; 

int maxSum(int stack1[], int stack2[], int stack3[], int n1, int n2, int n3){ 
    int sum1 = 0, sum2 = 0, sum3 = 0; 
    
    for(int i=0; i < n1; i++){ 
        sum1 += stack1[i]; 
    }      

    for(int i=0; i < n2; i++){ 
        sum2 += stack2[i]; 
    } 
    
    for(int i=0; i < n3; i++){ 
        sum3 += stack3[i]; 
    }
    
    int top1 =0, top2 = 0, top3 = 0;
    
    while(1){ 
        if((top1 == n1) || (top2 == n2) || (top3 == n3)){ 
            return 0; 
        }
        
        if((sum1 == sum2) && (sum2 == sum3)){ 
            return sum1; 
        }
        
        if((sum1 >= sum2) && (sum1 >= sum3)){ 
            sum1 -= stack1[top1++]; 
        }
        
        else if((sum2 >= sum3) && (sum2 >= sum3)){ 
            sum2 -= stack2[top2++]; 
        }
        
        else if(sum3 >= sum2 && sum3 >= sum1){ 
            sum3 -= stack3[top3++]; 
        }
    } 
} 
int main(){

    int stack1[] = {3, 2, 1, 1, 1}; 
    int stack2[] = {4, 3, 2}; 
    int stack3[] = {1, 1, 4, 1}; 
    
    int n1 = sizeof(stack1)/sizeof(stack1[0]); 
    int n2 = sizeof(stack2)/sizeof(stack2[0]); 
    int n3 = sizeof(stack3)/sizeof(stack3[0]); 
    
    cout << maxSum(stack1, stack2, stack3, n1, n2, n3) << endl; 
    
    return 0; 
}
5

Java Program to find maximum sum possible equal sum of three stacks

class MaxPossibleSum{ 

    public static int maxSum(int stack1[], int stack2[], int stack3[], int n1, int n2, int n3){ 
        int sum1 = 0, sum2 = 0, sum3 = 0; 
        
        for(int i=0; i < n1; i++){ 
            sum1 += stack1[i]; 
        } 
        
        for(int i=0; i < n2; i++){ 
            sum2 += stack2[i]; 
        }
        
        for(int i=0; i < n3; i++){ 
            sum3 += stack3[i]; 
        }
        
        int top1 =0, top2 = 0, top3 = 0; 
        int ans = 0; 
        
        while (true){ 
        
            if((top1 == n1) || (top2 == n2) || (top3 == n3)){ 
                return 0; 
            }
            
            if((sum1 == sum2) && (sum2 == sum3)){ 
                return sum1; 
            }
            
            if((sum1 >= sum2) && (sum1 >= sum3)){ 
                sum1 -= stack1[top1++]; 
            }
            
            else if((sum2 >= sum3) && (sum2 >= sum3)){ 
                sum2 -= stack2[top2++]; 
            }
            
            else if((sum3 >= sum2) && (sum3 >= sum1)){ 
                sum3 -= stack3[top3++]; 
            }
        } 
    } 
    
    public static void main(String[] args){
        int stack1[] = {3, 2, 1, 1, 1}; 
        int stack2[] = {4, 3, 2}; 
        int stack3[] = {1, 1, 4, 1}; 
        
        int n1 = stack1.length; 
        int n2 = stack2.length; 
        int n3 = stack3.length; 
        
        System.out.println(maxSum(stack1, stack2, stack3, n1, n2, n3)); 
    } 
}
5

Complexity Analysis

Time Complexity: O(n1+n2+n3) where n1, n2, and n3 are the number of elements in arrays stack1, stack2, and stack3 respectively.

Auxiliary Space: O(1) as we are using constant space.

References

Translate »