In prefix to postfix conversion problem, we have given expression in prefix notation in string format. Write a program to convert the given notation in postfix notation.
Prefix Notation
In this notation, we write the operands after the operator. It is also known as Polish Notation.
For instance: +AB is a prefix expression.
Postfix Notation
In this notation, the operands are written before the operator. It is also known as Reverse Polish Notation.
For instance: AB+ is a postfix expression.
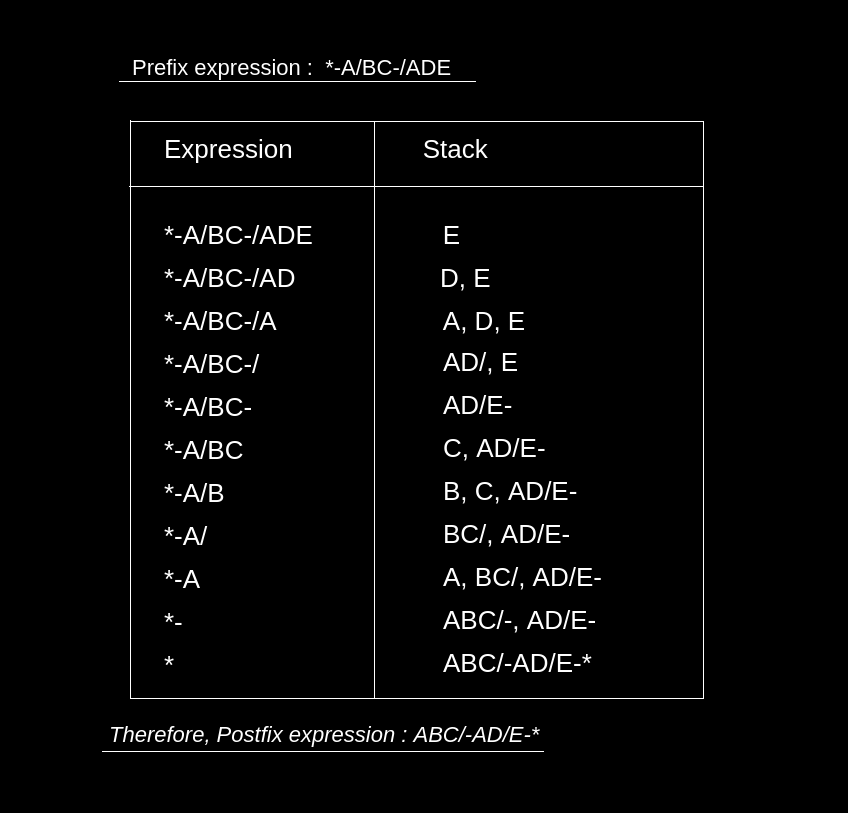
Table of Contents
Example
Input : Prefix : *-A/BC-/ADE
Output : Postfix : ABC/-AD/E-*
Input : Prefix : *+AB-CD
Output : Postfix : AB+CD-*
Algorithm for Prefix to Postfix Conversion
- Initialize a string containing prefix expression.
- Create a stack s of type string.
- Traverse from the last character to first of the string and check if the current character is an operator pop the two top characters from the stack and concatenate them as a single string with current operator after these both. Push the string back into the stack.
- Else if the current character is not an operator, push it as a string in the stack.
- Return the top of the stack.
Implementation
C++ Program for Prefix to Postfix Conversion
#include <iostream>
#include <stack>
using namespace std;
bool isOperator(char x){
switch (x){
case '+':
case '-':
case '/':
case '*':
return true;
}
return false;
}
string prefixToPostfix(string prefix_exp){
stack<string> s;
int l = prefix_exp.size();
for(int i = l-1; i >= 0; i--){
if(isOperator(prefix_exp[i])){
string op1 = s.top();
s.pop();
string op2 = s.top();
s.pop();
string temp = op1 + op2 + prefix_exp[i];
s.push(temp);
}
else{
s.push(string(1, prefix_exp[i]));
}
}
return s.top();
}
int main(){
string prefix_exp = "*-A/BC-/ADE";
cout<<"Postfix : "<<prefixToPostfix(prefix_exp);
return 0;
}Postfix : ABC/-AD/E-*
Java Program for Prefix to Postfix Conversion
import java.util.*;
class Prefix{
static boolean isOperator(char x){
switch (x){
case '+':
case '-':
case '/':
case '*':
return true;
}
return false;
}
static String prefixToPostfix(String prefix_exp){
Stack<String> s= new Stack<String>();
int l = prefix_exp.length();
for(int i = l-1; i >= 0; i--){
if(isOperator(prefix_exp.charAt(i))){
String op1 = s.peek();
s.pop();
String op2 = s.peek();
s.pop();
String temp = op1 + op2 + prefix_exp.charAt(i);
s.push(temp);
}
else{
s.push(prefix_exp.charAt(i)+"");
}
}
return s.peek();
}
public static void main(String args[]){
String prefix_exp = "*-A/BC-/ADE";
System.out.println("Postfix : " + prefixToPostfix(prefix_exp));
}
}Postfix : ABC/-AD/E-*
Complexity Analysis
Time Complexity: O(n) where n is the length of the prefix string.
Space Complexity: O(n) as we use space to store each of the n characters of the string.