Table of Contents
Problem Statement
The problem “Sort a stack using a temporary stack” states that you are given a stack data structure. Sort the elements of the given stack using a temporary stack.
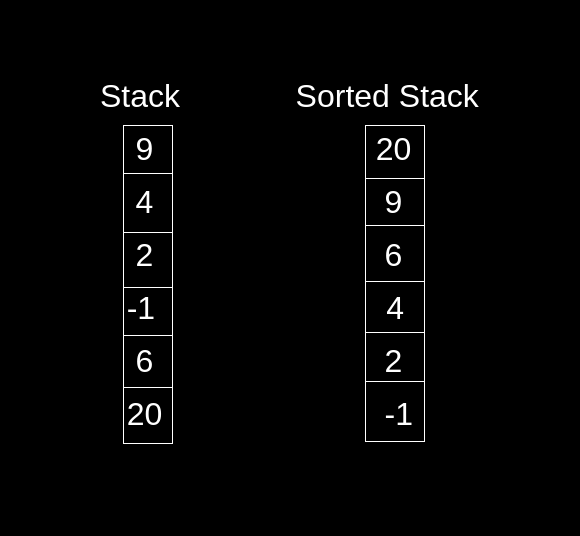
Example
9 4 2 -1 6 20
20 9 6 4 2 -1
2 1 4 3 6 5
6 5 4 3 2 1
For instance
Let Stack = [9 4 2 -1 6 20] and Temporary stack = []
Steps for sorting - 1.Top of stack = 20 Stack = [9 4 2 -1 6] Temporary stack = [20] 2. Top of stack = 6 Stack = [9 4 2 -1 20] Temporary stack = [6] 3. Top of stack = 20 Stack = [9 4 2 -1] Temporary stack = [6 20] 4. Top of stack = -1 Stack = [9 4 2 20 6] Temporary stack = [-1] 5. Top of stack = 6 Stack = [9 4 2 20] Temporary stack = [-1 6] 6. Top of stack = 20 Stack = [9 4 2] Temporary stack = [-1 6 20] 7. Top of stack = 2 Stack = [9 4 20 6] Temporary stack = [-1 2] 8. Top of stack = 6 Stack = [9 4 20] Temporary stack = [-1 2 6] 9. Top of stack = 20 Stack = [9 4] Temporary stack = [-1 2 6 20] 10. Top of stack = 4 Stack = [9 20 6] Temporary stack = [-1 2 4] 11. Top of stack = 6 Stack = [9 20] Temporary stack = [-1 2 4 6] 12. Top of stack = 20 Stack = [9] Temporary stack = [-1 2 4 6 20] 13. Top of stack = 9 Stack = [20] Temporary stack = [-1 2 4 6 9] 14. Top of stack = 20 Stack = [] Temporary stack = [-1 2 4 6 9 20]
As the Stack is empty and the temporary stack is in sorted, print the temporary stack starting from it’s top.
Therefore, Output : 20 9 6 4 2 -1
Algorithm to Sort a stack using a temporary stack
- Initialize a stack data structure and insert/push the elements in it.
- After that create a function sort() which accepts a stack as it’s parameter. Initialize another temporary/auxiliary stack tmpStack in it.
- Traverse while the original stack is not empty, create a variable tmp and store the top of the original stack in it. After that pop the top of the original stack.
- Again Traverse while tmpStack is not empty and the top of the tmpStack i.e. the temporary stack is greater not less than or equal to the variable tmp, push the top of the temporary stack in the original stack and pop the top of the temporary stack.
- Push variable tmp in the temporary stack.
- While the temporary stack is not empty, print it’s top and pop it’s top.
Code
C++ Program to sort a stack using recursion
#include <iostream>
#include <stack>
using namespace std;
stack<int> sort(stack<int> &input){
stack<int> tmpStack;
while(!input.empty()){
int tmp = input.top();
input.pop();
while(!tmpStack.empty() && tmpStack.top() > tmp){
input.push(tmpStack.top());
tmpStack.pop();
}
tmpStack.push(tmp);
}
return tmpStack;
}
int main(){
stack<int> input;
input.push(20);
input.push(6);
input.push(-1);
input.push(2);
input.push(4);
input.push(9);
stack<int> tmpStack = sort(input);
while (!tmpStack.empty()){
cout << tmpStack.top()<< " ";
tmpStack.pop();
}
}20 9 6 4 2 -1
Java Program to sort a stack using recursion
import java.util.*;
class SortStack{
public static Stack<Integer> sort(Stack<Integer> input){
Stack<Integer> tmpStack = new Stack<Integer>();
while(!input.isEmpty()){
int tmp = input.pop();
while(!tmpStack.isEmpty() && tmpStack.peek() > tmp){
input.push(tmpStack.pop());
}
tmpStack.push(tmp);
}
return tmpStack;
}
public static void main(String args[]){
Stack<Integer> input = new Stack<Integer>();
input.add(20);
input.add(6);
input.add(-1);
input.add(2);
input.add(4);
input.add(9);
Stack<Integer> tmpStack=sort(input);
while (!tmpStack.empty()){
System.out.print(tmpStack.pop()+" ");
}
}
}20 9 6 4 2 -1
Complexity Analysis
Time Complexity
O(n^2) where n is the number of elements in the stack. Since we are pushing the elements back from the temporary stack to the original stack in case the top of the temporary stack is lesser than the element to be pushed. For better understanding, consider a descending order sequence and try to run the algorithm.
Space Complexity
O(n) because we used temporary stack space for n elements. The space used by the original stack is not counted for the algorithm.