Rabin Karp Algorithm used to find the pattern string in the given text string. There are so many types of algorithms or methods used to find the pattern string. In this algorithm, we use Hashing for finding the pattern matching. If we got the same hash code for the substring and pattern string then we check the digits else move to the next substring. We find the hash code for the string using some code values of a character. Let’s see an example for better understanding.
Hash code for the characters is listed below.
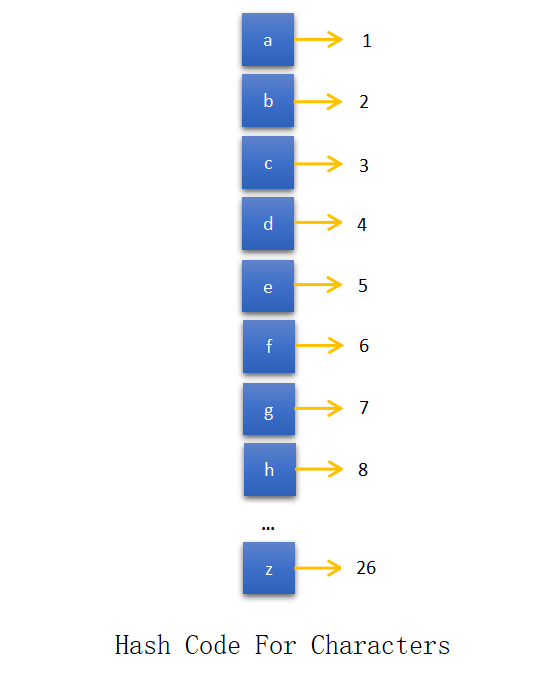
Table of Contents
Working of Rabin Karp Algorithm
Step-1
Find the hash code value of pattern string using the hash code assigned for characters.
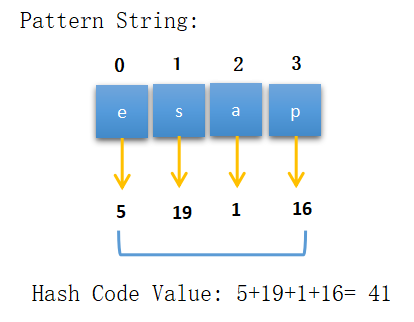
Step-2
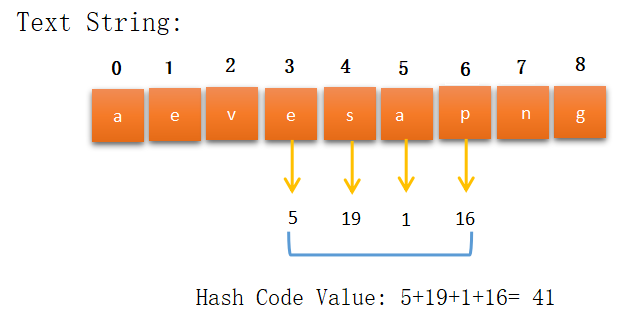
If M is the length of the pattern string then we start taking M length substring from the beginning of the text string. After it, find the hash code value for the substring and check if it’s matching with the hash code value of the pattern string. If its match then checks the character one by one else moves to the next substring.

Hash code value is not the same then we move to the next substring of length M(4).
Step-3

Hash code value is not the same then we move to the next substring of length M.
Step-4

Hash code value is not the same here also, so we move to the next substring.
Step-5
Hash code value is the same here, so we check the substring characters one by one with the pattern string.

All the characters matched then we print the starting index of the substring and move to the next substring of length M if possible.
Step-6

The value of the hash code of current substring not matched with the hash code value of the pattern string. So, move to the next substring of length M if possible else stop.
Step-7
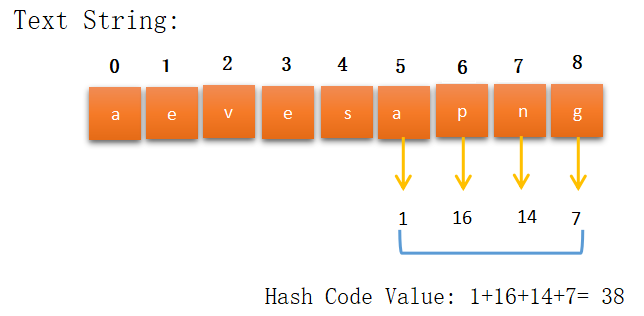
Hash code value not matched here also and this is the final substring of length M. So, we stop our process here.
Note: There are different ways to create or define the hash function here i take a simple hash function to better understanding. In the implementation part, i make the hash function such that it is effective to find the hash code value in O(1) time.
Algorithm
Step:1 Find the hash code value of the given pattern string of length M.
Step:2 For i in range 1 to N-M+1:
i) Find the hash code value using hash function.
ii) Check if the hash code match to the pattern string hash code value then print the starting index of substring.
iii) If not matching then move to the next substring.
Implementation
/*C++ Implementation of Rabin Karp Algorithm.*/
#include<bits/stdc++.h>
using namespace std;
/*function to find the pattern in effective way*/
void rabin_karp(string &text,string &pattern, int q)
{
/*length of the pattern string*/
int m = pattern.length();
/*length of the text string*/
int n = text.length();
int p=0,t=0,h=1,d=26;// here p is the hash value for pattern and t is the hash value of the substring;
/*h=pow(d,M-1) where d is 26 if the text contain only lowe case characters.*/
for(int i=0;i<m-1;i++)
{
h=(h*d)%q;
}
/*calculate the hash value for the pattern string and the first substring of length m*/
for(int i=0;i<m;i++)
{
p=(d*p+pattern[i])%q;//pattern string;
t=(d*t+text[i])%q;//substring;
}
/*for remaining substring of length m*/
for(int i=0;i<=n-m;i++)
{
/*if hash values are same then check charachter by character in substring and pattern string.*/
if(p==t)
{
int flag=0;
for(int j=0;j<m;j++)
{
if(text[i+j]!=pattern[j])
{
flag=1;
break;
}
}
/*if all the character are match then print the starting index of substring.*/
if(flag==0)
{
cout<<"Pattern found at index: "<<i+1<<endl;
}
}
/*find the hash value of the next substring by removinf the first character from previos substring
and add next char to the end of the previous string*/
/*it take O(1) time to find the hash values*/
if(i<n-m)
{
t=(d*(t-text[i]*h)+text[i+m])%q;
if(t<0)
{
t=(t+q);
}
}
}
}
int main()
{
/*input values*/
string text;
cin>>text;
string pattern;
cin>>pattern;
rabin_karp(text,pattern,97);
return 0;
}Input-1: aevesapng esap
Output-1: Pattern found at index: 4
Input-2: asadschdgdcaadvadwhemvaadvdeaadvs aadv
Output-2: Pattern found at index: 12 Pattern found at index: 23 Pattern found at index: 29
Time Complexity
O(N*M) is the worst-case time complexity in which all the substring is equal to the pattern string. Its because we check character by character once the hash value is the same so its takes O(M) time to check each substring. Best and Average time complexity is O(N+M) where N is the length of the text string and M is the length of the pattern string.
Space Complexity
O(1) is the space complexity means here we don’t use any extra space to find the result. We just find the hash value and store them into variables. So, here we used a few variables which means we do not use the memory of big size.