In repeated substring patterns we have given a string check if it can be constructed by taking a substring of itself and appending multiple copies of the substring together.
Table of Contents
Example
Input 1: str = “abcabcabc” Output: True Explanation: “abcabcabc” can be formed by repeatedly appending “abc” to an empty string. Input 2: str = “xyxy” Output: True Explanation: “xyxy” can be formed by repeatedly appending “xy” to an empty string. Input 3: str = “xyzxy” Output: False Explanation: str has no such substring that can be repeatedly appended to an empty string to form str. Input 4: str = “Tutorialcup” Output: False
Types of solution for repeated substring pattern
- KMP algorithm
- substring search
KMP algorithm
Approach for repeated substring pattern
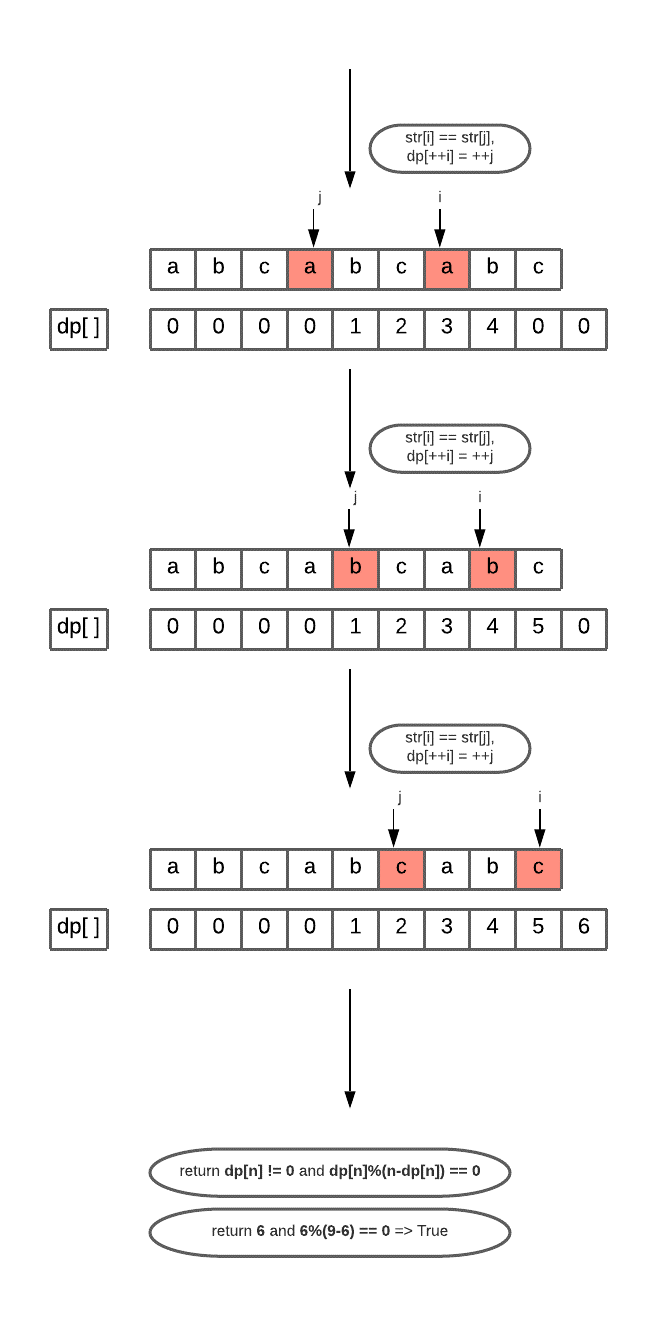
We use the KMP algorithm to find the longest prefix lps which is also the suffix of the given string. If the length of the input string is some multiple lps and last character of the string matches with the last character of the lps string. Then we have a substring (which is lps itself) of the input string which when repeated (or appended) a certain number of times gives the input string itself.
We will construct an array dp[ ], where dp[i+1] stores length of the longest prefix which is also a suffix up to index i. After which we will check using dp[ ] if there exists any such substring of the input string.
To calculate dp[i], we are using values from dp[i-1 … 0], so this is a dynamic programming approach.
Algorithm
- Construct an array dp[ ] of length = n+1, where n = string length. dp[i+1] denotes the length of the longest proper prefix of the string which is also a suffix up to the index = i.
- initiate two pointers j = 0 and i = 1, j is used to track the last character of the longest proper prefix, LPP (also a suffix), i is used to tracking the current character during the traversal.
- Begin traversing the string from left to right using i as the loop variable.
- if str[i] == str[j] => dp[++i] == ++j, if last character of LPP and current character match, simply increase the length of LPP by 1.
- Else if the characters don’t match:
- if length of LPP is 0 so far, then even first (str[0]) and current (str[i]) character don’t match => dp[i] = 0.
- if length of LPP is not 0, then simply recur => j = dp[j].
- After the traversal is over, return if the input string length is divisible by LPP length.

Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/* function that checks if the input string can be generated
by repeatedly adding a substring of the input string */
bool hasRepeatedSubstring(string str)
{
int i = 1, j = 0, n = str.size();
/* dp[i+1] stores longest proper prefix
upto index i which also a suffix */
vector <int> dp(n+1,0);
/* Traverse the string */
while(i < n)
{
/* if the current character (at index = i) is same as the last
character of longest common prefix obtained upto index i-1 */
if(str[i] == str[j])
dp[++i] = ++j;
/* if characters don't match */
else
{
/* when str[0] and str[i] don't match no proper
prefix which is also a suffix is possible
so length is 0, simply move on to next character*/
if(j == 0)
i++;
/* decrease the length (by 1) of longest proper
prefix (also suffix) possible upto index i-1
and then match the last character of longest
proper prefix to character at current index */
else
j = dp[j];
}
}
/* check if there is any such prefix of
input string that has length that
completely divides the input string length */
return dp[n] && (dp[n]%(n-dp[n]) == 0);
}
int main()
{
/* input string */
string str = "abcabcabc";
if(hasRepeatedSubstring(str))
cout<<"Formed by repeating substring";
else
cout<<"Cannot be formed by repeated substring";
return 0;
}Formed by repeating substring
Java Program
import java.util.*;
import java.io.*;
class TutorialCup
{
/* function that checks if the input string can be generated
by repeatedly adding a substring of the input string */
static boolean hasRepeatedSubstring(String str)
{
int i = 1, j = 0, n = str.length();
/* dp[i+1] stores longest proper prefix
upto index i which also a suffix */
int [] dp = new int[n+1];
/* Traverse the string */
while(i < n)
{
/* if the current character (at index = i) is same as the last
character of longest common prefix obtained upto index i-1 */
if(str.charAt(i) == str.charAt(j))
dp[++i] = ++j;
/* if characters don't match */
else
{
/* when str[0] and str[i] don't match no proper
prefix which is also a suffix is possible
so length is 0, simply move on to next character*/
if(j == 0)
i++;
/* decrease the length (by 1) of longest proper
prefix (also suffix) possible upto index i-1
and then match the last character of longest
proper prefix to character at current index */
else
j = dp[j];
}
}
/* check if there is any such prefix of
input string that has length that
completely divides the input string length */
return dp[n] != 0 && (dp[n]%(n-dp[n]) == 0);
}
public static void main (String[] args)
{
/* input string */
String str = "abcabcabc";
if(hasRepeatedSubstring(str))
System.out.print("Formed by repeating substring");
else
System.out.print("Cannot be formed by repeated substring");
}
}Formed by repeating substring
Complexity Analysis for repeated substring pattern
- Time Complexity: T(n) = O(n), single traversal of the input string is done.
- Space Complexity: A(n) = O(n), for the dp[ ] array used.
Substring Search
Approach for repeated substring pattern
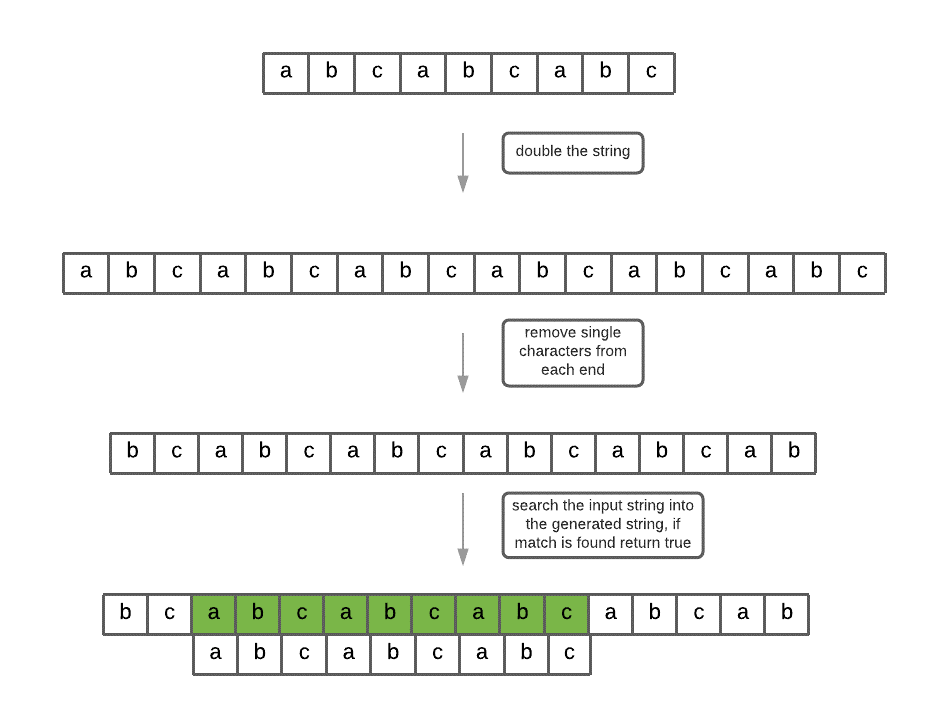
If the original string has a repeating substring, the repeating substring can be no larger than 1/2 the length of the original string. Ex: “abcabc” would be “abc”.
By doubling the input string and removing the first and last character, i.e. “abcabcabcabc” => “bcabcabcab”, if the original string “abcabc” can be found in “bcabcabcab”, it means that “abcabc” is made up by repeating one of its a substring.
Algorithm
- Construct a string pattern adding the input string str twice.
- Remove the first and last characters in the pattern.
- Find for str in the pattern, if the match is found return True else return False.
Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/* function that checks if the input string can be generated
by repeatedly adding a substring of the input string */
bool hasRepeatedSubstring(string str)
{
string pattern = str.substr(1) + str.substr(0,str.length()-1);
return pattern.find(str) != string::npos;
}
int main()
{
/* input string */
string str = "abcabcabc";
if(hasRepeatedSubstring(str))
cout<<"Formed by repeating substring";
else
cout<<"Cannot be formed by repeated substring";
return 0;
}Formed by repeating substring
Java Program
import java.util.*;
import java.io.*;
class TutorialCup
{
/* function that checks if the input string can be generated
by repeatedly adding a substring of the input string */
static boolean hasRepeatedSubstring(String str)
{
int n = str.length();
String pattern = str.substring(1) + str.substring(0,n-1);
return pattern.contains(str);
}
public static void main (String[] args)
{
/* input string */
String str = "abcabcabc";
if(hasRepeatedSubstring(str))
System.out.print("Formed by repeating substring");
else
System.out.print("Cannot be formed by repeated substring");
}
}Formed by repeating substring
Complexity Analysis for repeated substring pattern
- Time complexity: T(n) = O(n), for sub string search.
- Space Complexity: A(n) = O(n), for generating the pattern string out of input string.