Table of Contents
Problem Statement
The problem “Binary Search Tree Delete Operation” asks us to implement the delete operation for binary search tree. Delete function refers to the functionality to delete a node with a given key/data.
Example
Input
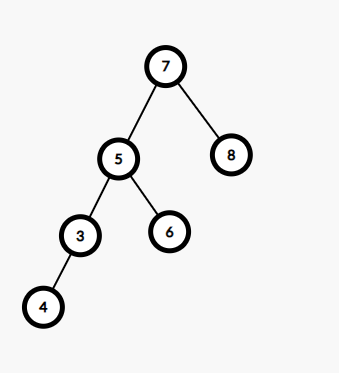
Node to be deleted = 5
Output

Approach for Binary Search Tree Delete Operation
So when we talk about deleting a node from a binary search tree. One thing to note is whenever we delete a node, all the properties of BST must be kept satisfied. If we are removing an internal node, we need to make sure that subtree along with the new root satisfies the properties of BST.
Now, we have three cases to deal with. These cases are based on the number of children a node have. And to answer the question why are categorizing the nodes on the basis of number of children? So, it’s easier to deal with a lead and a node with single child. So let’s discuss all the three cases briefly.
- Node with no child (leaf)
- Node with single child
- Node with two children
If the node is a leaf, we can simply remove the node from the tree. This operation can not result in violation of any of the BST properties. Now if we consider the case of a single child. We can simply remove the node and place its child in it’s place. The only problem arises when we try to remove a node with two children.
To remove a node having two children, first we find the inorder successor of this node. Place the successor in the place of the node being removed. Now how can we guarantee removing the successor will not violate the BST properties? We can guarantee this because a node which happens to be the successor can never have two children. Either it will have one child or no child at all. So removing the successor will not violate the BST properties.
Code
C++ code for Binary Search Tree Delete Operation
#include<bits/stdc++.h>
using namespace std;
struct node
{
int data;
node *left, *right;
};
node* create(int data){
node* tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
}
void inorder(node* root){
if(root){
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
// return the node which is in the most left direction of root
// the smallest node in the entire subtree rooted at current node
node* minNode(node* root)
{
node* tmp = root;
while(tmp && tmp->left)
tmp = tmp->left;
return tmp;
}
// deleted the node with given data from tree
node* deleteNode(node* root, int data)
{
// if current node is empty return current node(NULL)
if(!root) return root;
// node to be deleted is in left sub-tree
if (data < root->data)
root->left = deleteNode(root->left, data);
// node to be deleted in right sub-tree
else if (data > root->data)
root->right = deleteNode(root->right, data);
// current node is node to be deleted
else
{
// Case 1 + Case 2
// if left is null this means that it is either of the two cases
if (root->left == NULL)
{
node* tmp = root->right;
free(root);
return tmp;
}
// Case 2 node has a left child but not right child
// thus it has only a single child
else if (root->right == NULL)
{
node* tmp = root->left;
free(root);
return tmp;
}
// Case 3
// first find the successor
// successor is the element which comes next in inorder traversal of BST
// so it is the node in most left direction in right sub-tree
node *successor = minNode(root->right);
// place successor in place of current node
root->data = successor->data;
// now simply delete the successor from root's right child
root->right = deleteNode(root->right, successor->data);
}
return root;
}
int main()
{
node* root = create(7);
root->left = create(5);
root->right = create(8);
root->left->left = create(3);
root->left->left->right = create(4);
root->left->right = create(6);
cout<<"current inorder traversal of tree"<<endl;
inorder(root);
cout<<endl;
root = deleteNode(root, 5);
cout<<"inorder traversal after deleting node with value 5"<<endl;
inorder(root);
cout<<endl;
return 0;
}
current inorder traversal of tree 3 4 5 6 7 8 inorder traversal after deleting node with value 5 3 4 6 7 8
Java code for Binary Search Tree Delete Operation
import java.util.*;
// Class that denotes a node of the tree
class node
{
int data;
node left, right, random;
public node(int data)
{
this.data = data;
left = right = random = null;
}
}
class Tree
{
static node root;
static node create(int data) {
node tmp = new node(data);
return tmp;
}
static void inorder(node root){
if(root != null){
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
// return the node which is in the most left direction of root
// the smallest node in the entire subtree rooted at current node
static node minNode(node root)
{
node tmp = root;
while(tmp != null && tmp.left != null)
tmp = tmp.left;
return tmp;
}
// deleted the node with given data from tree
static node deleteNode(node root, int data)
{
// if current node is empty return current node(NULL)
if(root == null) return root;
// node to be deleted is in left sub-tree
if (data < root.data)
root.left = deleteNode(root.left, data);
// node to be delted in right sub-tree
else if (data > root.data)
root.right = deleteNode(root.right, data);
// current node is node to be deleted
else
{
// Case 1 + Case 2
// if left is null this means that it is either of the two cases
if (root.left == null)
{
return root.right;
}
// Case 2 node has a left child but not right child
// thus it has only a single child
else if (root.right == null)
{
return root.left;
}
// Case 3
// first find the successor
// successor is the element which comes next in inorder traversal of BST
// so it is the node in most left direction in right sub-tree
node successor = minNode(root.right);
// place successor in place of current node
root.data = successor.data;
// now simply delete the successor from root's right child
root.right = deleteNode(root.right, successor.data);
}
return root;
}
public static void main(String[] args)
{
root = create(7);
root.left = create(5);
root.right = create(8);
root.left.left = create(3);
root.left.left.right = create(4);
root.left.right = create(6);
System.out.println("current inorder traversal of tree");
inorder(root);
System.out.println();
root = deleteNode(root, 5);
System.out.println("inorder traversal after deleting node with value 5");
inorder(root);
System.out.println();
}
}current inorder traversal of tree 3 4 5 6 7 8 inorder traversal after deleting node with value 5 3 4 6 7 8
Complexity Analysis
Time Complexity
O(N), for deleting. Consider you need to delete the tree’s root which has left and right children. And the right children is a skewed tree in left direction after the immediate right child of root. So this makes the delete operation to run in linear time complexity.
Space Complexity
O(1), during delete operation. We have not stored any information and thus making the algorithm to take constant space.
There exists an optimization to the above approach but that also takes O(N) time. We can run an inorder traversal and save parent of each node. This way when we need to delete successor we simply replace its parent’s left or right child to null accordingly. But that approach will take O(N) space and will not affect the worst-case time complexity.