Table of Contents
Problem Statement
Given an array with n elements, check given array of size n can represent BST of n levels or not. That is to check whether the binary search tree constructed using these n elements can represent a BST of n levels.
Examples
arr[] = {10, 8, 6, 9, 3}false
Explanation: Since 8, and 9 will be placed on same level in BST. We will not be able to get a BST of n levels.
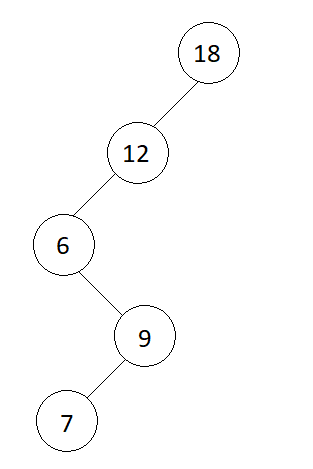
arr[] = {18, 12, 6, 9, 7}true
Explanation: Here, as shown in above picture no two elements are on same level. Thus, we are left with a BST of n size.
Approach
Method 1 (By Constructing the Tree)
One of the way to solve above problem is to construct a tree with n levels from the given array by inserting the value smaller than current node on the left of current node and value greater than current node on the right of current node.
After constructing the tree, we check whether the tree is binary search tree or not, if it is a Binary Search Tree, then the output is true, else the output is false. If is true then we have checked whether a given array of size n can represent BST of n levels or not, and found that it can.
1. Initialize root as the first element of the given array. Also initialize temp as root. 2. Traverse the given array starting from index 1(0-based indexing), if the current element is less than temp's value insert it to the left of temp and make temp as left of temp, else insert the current element to the right of temp and make temp as right of temp. 3. After building the tree with n levels using step 2, check if the constructed tree is BST or not. If it is BST return true, else return false.
Complexity Analysis
Time Complexity = O(n), since we are traversing through whole input of size n.
Space Complexity = O(h), here we are creating a node for each element in input array. Thus making a total of n nodes contributes to linear space complexity.
where n is the number of elements in the array and h is the height of BST, in this case h is equals to n.
JAVA Code
import java.util.*;
import java.lang.*;
import java.io.*;
class CheckGivenArrayOfSizenCanRepresentBSTOfnLevelsOrNot {
// class to represent the node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to check if a tree is BST or not
private static boolean isBST(Node root, int min, int max) {
if (root == null) {
return true;
}
return (root.data < max && root.data > min) &&
isBST(root.left, min, root.data) &&
isBST(root.right, root.data, max);
}
private static Node constructNLevelTree(int[] arr) {
// initialize root as first element of array
Node root = new Node(arr[0]);
// initialize temp as root
Node temp = root;
// traverse the array from index 1
for (int i = 1; i < arr.length; i++) {
// if current element is less than temp, make temp's left as current element
// and temp as temp's left
if (arr[i] < temp.data) {
temp.left = new Node(arr[i]);
temp = temp.left;
}
// else, make temp's right as current element
// and temp as temp's right
else {
temp.right = new Node(arr[i]);
temp = temp.right;
}
}
// return the root of tree formed
return root;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[] {10, 8, 6, 9, 3};
Node root1 = constructNLevelTree(arr1);
System.out.println(isBST(root1, Integer.MIN_VALUE, Integer.MAX_VALUE));
// Example 2
int arr2[] = new int[] {18, 12, 6, 9, 7};
Node root2 = constructNLevelTree(arr2);
System.out.println(isBST(root2, Integer.MIN_VALUE, Integer.MAX_VALUE));
}
}
false true
C++ Code
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
bool isBST(Node *root, int min, int max) {
if (root == NULL) {
return true;
}
return (root->data < max && root->data > min &&
isBST(root->left, min, root->data) &&
isBST(root->right, root->data, max));
}
Node* constructNLevelTree(int *arr, int n) {
// initialize root as first element of array
Node *root = new Node(arr[0]);
// initialize temp as root
Node *temp = root;
// traverse the array from index 1
for (int i = 1; i < n; i++) {
// if current element is less than temp, make temp's left as current element
// and temp as temp's left
if (arr[i] < temp->data) {
temp->left = new Node(arr[i]);
temp = temp->left;
}
// else, make temp's right as current element
// and temp as temp's right
else {
temp->right = new Node(arr[i]);
temp = temp->right;
}
}
// return the root of tree formed
return root;
}
int main() {
// Example 1
int arr1[] = {10, 8, 6, 9, 3};
Node *root1 = constructNLevelTree(arr1, sizeof(arr1) / sizeof(arr1[0]));
if (isBST(root1, INT_MIN, INT_MAX)) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 2
int arr2[] = {18, 12, 6, 9, 7};
Node *root2 = constructNLevelTree(arr2, sizeof(arr2) / sizeof(arr2[0]));
if (isBST(root2, INT_MIN, INT_MAX)) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}false true
Method 2 (Without Constructing Tree)
Check given array of size n can represent BST of n levels or not problem can also be solved in constant space complexity. The idea is to maintain two variables min and max that ensures the condition of minimum and maximum values for the upcoming element to be present in a new level. That is, the element should lie between min and max to be present in a new level, otherwise it will be inserted in some existing level in the tree.
1. Initialize min as -infinity and max as infinity. 2. Traverse the given array from index 1(0-based indexing). 3. If the current element is greater than prev element, and also it lies in the range min and max, then update min as prev element. 4. Else if the current element is smaller than prev element and it lies in the range min and max, then update max as prev element. 5. If none of the conditions in step 3 and step 4 is true, return false. 6. At the end of traversal return true.
Complexity Analysis
Time Complexity = O(n), since we are traversing through whole input of size n.
Space Complexity = O(1), since we are not creating nodes for each element. And have used only a particular number of variables, we have constant space solution.
where n is the number of elements in the array.
JAVA Code
import java.util.*;
import java.lang.*;
import java.io.*;
class CheckGivenArrayOfSizenCanRepresentBSTOfnLevelsOrNot {
private static boolean canRepresent(int[] arr) {
// initialise min as -infinity and max as infinity
int min = Integer.MIN_VALUE, max = Integer.MAX_VALUE;
// traverse the array from index 1
for (int i = 1; i < arr.length; i++) {
// if current element is greater than prev and lies in the
// range min and max, update min as prev
if (arr[i] > arr[i - 1] && arr[i] > min && arr[i] < max) {
min = arr[i - 1];
}
// else if current element is less than prev and lies in the
// range min and max, update max as prev
else if (arr[i] < arr[i - 1] && arr[i] > min && arr[i] < max) {
max = arr[i - 1];
}
// in all other cases return false
else {
return false;
}
}
// at the end of the traversal return true
return true;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[] {10, 8, 6, 9, 3};
System.out.println(canRepresent(arr1));
// Example 2
int arr2[] = new int[] {18, 12, 6, 9, 7};
System.out.println(canRepresent(arr2));
}
}false true
C++ Code
#include <bits/stdc++.h>
using namespace std;
bool canRepresent(int *arr, int n) {
// initialise min as -infinity and max as infinity
int min = INT_MIN, max = INT_MAX;
// traverse the array from index 1
for (int i = 0; i < n; i++) {
// if current element is greater than prev and lies in the
// range min and max, update min as prev
if (arr[i] > arr[i - 1] && arr[i] > min && arr[i] < max) {
min = arr[i - 1];
}
// else if current element is less than prev and lies in the
// range min and max, update max as prev
else if (arr[i] < arr[i - 1] && arr[i] > min && arr[i] < max) {
max = arr[i - 1];
}
// in all other cases return false
else {
return false;
}
}
// at the end of the traversal return true
return true;
}
int main() {
// Example 1
int arr1[] = {10, 8, 6, 9, 3};
if (canRepresent(arr1, sizeof(arr1) / sizeof(arr1[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 2
int arr2[] = {18, 12, 6, 9, 7};
if (canRepresent(arr2, sizeof(arr2) / sizeof(arr2[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}false true