Check if the given array can represent Level Order Traversal of Binary Search Tree

Difficulty Level Easy
Frequently asked in Amazon Citrix IBM Indeed Info Edge OYO Rooms Teradata
Binary Search Tree Binary Tree Queue Tree Tree TraversalViews 2789

Problem Statement

The problem “Check if the given array can represent Level Order Traversal of Binary Search Tree” states that you are given a level order traversal of the binary search tree. And using the level order traversal of the tree. We need to efficiently find if the level order traversal can represent a binary search tree or not?

Example

Level Order Traversal - {5 2 7 1 6 9 }
True

 

Check if the given array can represent Level Order Traversal of Binary Search Tree

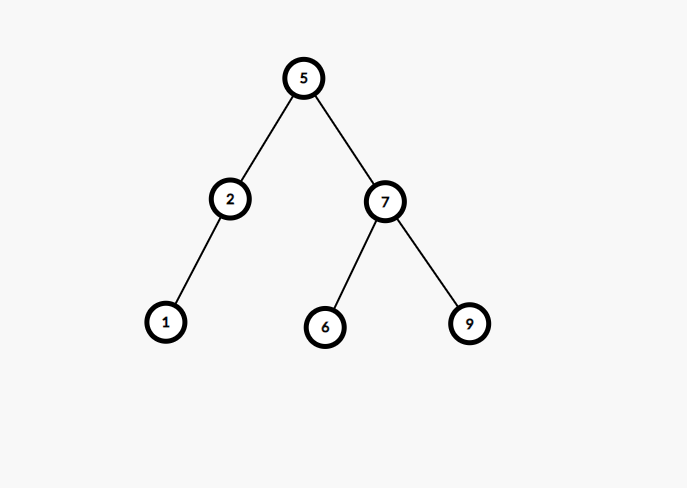
Explanation

The given level order traversal represents the binary tree which is shown in the image. And as we can see the tree satisfies all the properties of a binary tree and thus the output is true.

Approach to Check if the given array can represent Level Order Traversal of Binary Search Tree

Naive Approach

A naive approach could be if we try to make all the binary trees that satisfy the given level order traversal. And then check if the tree represents a binary search tree. But this operation will be very much costly. Like first of all, we will be constructing many trees. Then the algorithm requires checking if the tree formed is BST. So, we need to do something where we do not need to construct the tree.

Efficient Approach

An efficient approach will store the boundaries for each of the elements occurring in the level order traversal. These boundaries represent the boundary in which their subtree elements can lie. If we talk about a node, it will have a minimum and maximum. The left subtree can have elements ranging from minimum bound to the current node value-1. While the elements in the right subtree can range from the current node value+1 to maximum bound.

So, we will use a queue where we will keep on inserting the elements with these bounds and if we are able to traverse through all the nodes. We say that the given level order traversal can represent a BST else not. The algorithm is very similar to that of checking whether a binary tree is a BST or not?

Code

C++ code to Check if the given array can represent Level Order Traversal of Binary Search Tree

#include<bits/stdc++.h>
using namespace std;

struct node{
    int data;
    int mn;
    int mx;
};

node create(int data, int mn, int mx){
    node tmp;
    tmp.data = data;
    tmp.mn = mn;
    tmp.mx = mx;
    return tmp;
}

bool checkLevelOrderTraversalRepresentBinarySearchTree(vector<int> traversal){
    queue<node> q;
    int i = 0, n = traversal.size();
    q.push(create(traversal[i++], INT_MIN, INT_MAX));

    while(!q.empty()){
        node now = q.front();
        q.pop();
        if(i<n && now.mn<traversal[i] && traversal[i]<now.data)
            q.push(create(traversal[i++], now.mn, now.data));
        if(i<n && now.data<traversal[i] && traversal[i]<now.mx)
            q.push(create(traversal[i++], now.data, now.mx));
    }
    return (i == n);
}

int main()
{
    int t;cin>>t;
    while(t--){
        int n;cin>>n;
        vector<int> traversal(n);
        for(int i=0;i<n;i++)
            cin>>traversal[i];
        cout<<(checkLevelOrderTraversalRepresentBinarySearchTree(traversal) ? "true" : "no")<<endl;
    }
}

1
6
5 2 7 1 6 9
true

Java code to Check if the given array can represent Level Order Traversal of Binary Search Tree

import java.util.*;
import java.lang.*;
import java.io.*;

class node{
  int data;
  int mn;
  int mx;
}

class Main{
  
  static node create(int data, int mn, int mx){
      node tmp = new node();
      tmp.data = data;
      tmp.mn = mn;
      tmp.mx = mx;
      return tmp;
  }
  
  static boolean checkLevelOrderTraversalRepresentBinarySearchTree(int traversal[]){
      Queue<node> q = new LinkedList<node>();
      int i = 0; int n = traversal.length;
      q.add(create(traversal[i++], Integer.MIN_VALUE, Integer.MAX_VALUE));
  
      while(q.size() > 0){
          node now = q.peek();
          q.remove();
          if(i<n && now.mn<traversal[i] && traversal[i]<now.data)
              q.add(create(traversal[i++], now.mn, now.data));
          if(i<n && now.data<traversal[i] && traversal[i]<now.mx)
              q.add(create(traversal[i++], now.data, now.mx));
      }
      return (i == n);
  }
  
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
      int t = sc.nextInt();
      while(t-- > 0){
          int n = sc.nextInt();
          int[] traversal = new int[n];
          for(int i=0;i<n;i++)
              traversal[i] = sc.nextInt();
          System.out.println(checkLevelOrderTraversalRepresentBinarySearchTree(traversal) ? "true" : "no");
      }
  }
}
1
6
5 2 7 1 6 9
true

Complexity Analysis

Time Complexity

As we have simply traversed over the elements. And in the worst case, we need to traverse over all the elements, the algorithm has linear time complexity O(N).

Space Complexity

We have used a queue to store the elements which made the algorithm to have linear space complexity O(N).

Translate ยป