Given a pre-order traversal of a Binary Search Tree(BST), write an algorithm to construct the BST from given preorder traversal.
Table of Contents
Examples
Input
preOrder[] = {7, 5, 3, 6, 9}
Output
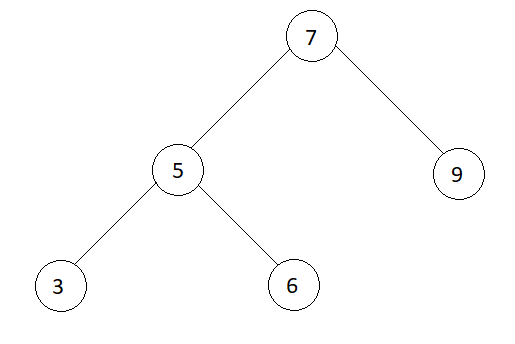
Inorder : 3 5 6 7 9
Input
preOrder[] = {12, 6, 1, 35, 20}
Output
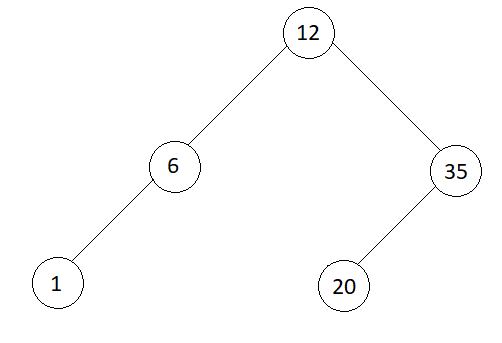
Inorder : 1 6 12 20 35
Naive Approach
We can see that the first element in the pre-order traversal is always the root of the tree and the rest of the elements are a part of the left and right sub-tree. As the tree is BST, so all the elements smaller than root are present in the left sub-tree, and elements greater than root are present in the right sub-tree.
So we traverse in the given array and find the first element greater than the root. Now the elements before this element(except root) is the pre-order traversal of left sub-tree and elements after this element(included it) is the pre-order traversal of right sub-tree.
So, the first element forms the root of BST, elements from index 1 to (i – 1) forms the left sub-tree, and elements from index i to (n – 1) forms the right sub-tree.
createBST(preOrder, low, high)
- The first element(preOrder[low]) in the array is the root of BST. If low is equals to high, return root.
- Traverse the array from index low + 1(0 based indexing) to high and find the first element greater than the root, let its index be i.
- Recursively call this method for elements from the index (low + 1) to (i – 1) and assign the BST formed to the left of root.
- Recursively call this method for elements from index i to high and assign the BST formed to the right of root.
- Return root.
Time Complexity = O(n2)
Space Complexity = O(n), due to recursion
where n is the size of the given pre-order array.
JAVA Code for Construct BST from given Preorder Traversal
public class ConstructBSTFromGivenPreorderTraversal {
// class representing Node of BST
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to print inorder of a Binary Tree
private static void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
private static Node createBST(int[] preOrder, int low, int high) {
// if there is only 1 node in the tree, this is root, return it
if (low == high) {
return new Node(preOrder[low]);
}
// the first node is the root of the BST
Node root = new Node(preOrder[low]);
// find the index of first element greater than root
int index = -1;
for (int i = low + 1; i <= high; i++) {
if (preOrder[i] > preOrder[low]) {
index = i;
break;
}
}
// if all the elements are smaller than root, they forms the left subtree
// and right subtree is null
if (index == -1) {
root.left = createBST(preOrder, low + 1, high);
root.right = null;
}
// else elements from index (low + 1) to (index - 1) forms the left subtree
// and elements from index 'index' to high forms the right subtree
else {
root.left = createBST(preOrder, low + 1, index - 1);
root.right = createBST(preOrder, index, high);
}
// return root
return root;
}
public static void main(String[] args) {
// Example 1
int preOrder1[] = new int[] {7, 5, 3, 6, 9};
Node root1 = createBST(preOrder1, 0, preOrder1.length - 1);
inorder(root1);
System.out.println();
// Example 2
int preOrder2[] = new int[] {12, 6, 1, 35, 20};
Node root2 = createBST(preOrder2, 0, preOrder2.length - 1);
inorder(root2);
System.out.println();
}
}3 5 6 7 9 1 6 12 20 35
C++ Code for Construct BST from given Preorder Traversal
#include <iostream>
#include<vector>
#include<queue>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to print the in-order traversal of a binary tree
void inOrder(Node *root) {
if (root != NULL) {
inOrder(root->left);
cout<<root->data<<" ";
inOrder(root->right);
}
}
Node* createBST(int *preOrder, int low, int high) {
// if there is only 1 node in the tree, this is root, return it
if (low == high) {
return new Node(preOrder[low]);
}
// the first node is the root of the BST
Node *root = new Node(preOrder[low]);
// find the index of first element greater than root
int index = -1;
for (int i = low + 1; i <=high; i++) {
if (preOrder[i] > preOrder[low]) {
index = i;
break;
}
}
// if all the elements are smaller than root, they forms the left subtree
// and right subtree is null
if (index == -1) {
root->left = createBST(preOrder, low + 1, high);
root->right = NULL;
}
// else elements from index (low + 1) to (index - 1) forms the left subtree
// and elements from index 'index' to high forms the right subtree
else {
root->left = createBST(preOrder, low + 1, index - 1);
root->right = createBST(preOrder, index, high);
}
// return root
return root;
}
int main() {
// Example 1
int preOrder1[] = {7, 5, 3, 6, 9};
Node *root1 = createBST(preOrder1, 0, (sizeof(preOrder1) / sizeof(preOrder1[0])) - 1);
inOrder(root1);
cout<<endl;
// Example 2
int preOrder2[] = {12, 6, 1, 35, 20};
Node *root2 = createBST(preOrder2, 0, (sizeof(preOrder2) / sizeof(preOrder2[0])) - 1);
inOrder(root2);
cout<<endl;
return 0;
}3 5 6 7 9 1 6 12 20 35
Optimal Approach
Recursive Method for Construct BST from given Preorder Traversal
The optimal idea here is to use the range trick, that is, we set a range for all the nodes, the node that comes in the range forms a root of the tree.
Initially, the range is -infinity(min) and +infinity(max), so the first root comes in the range and it forms a root. Then we call the same method for the left child(updated range is from min to root’s value) and for the right child(updated range is from root’s value to max).
createBST(min, max)
- If the value of the element at the currIndex(globally defined) is in between min and max(both not included), then it forms a root. Allocate memory and create a new node named root. Else jump to step 4.
- Increment currIndex and recursively call this method to form left sub-tree as, constructBST(min, root’s value).
- Recursively call this method to form the right subtree as, constructBST(root’s value, max).
- Return root.
Time Complexity = O(n)
Space Complexity = O(n)
where n is the size of the pre-order array.
JAVA Code for Construct BST from given Preorder Traversal
public class ConstructBSTFromGivenPreorderTraversal {
// class representing Node of BST
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// globally defined currIndex integer
private static int currIndex = 0;
// function to print inorder of a Binary Tree
private static void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
private static Node createBST(int[] preOrder, int min, int max) {
if (currIndex >= preOrder.length) {
return null;
}
Node root = null;
// if current element is in between min and max
if (preOrder[currIndex] > min && preOrder[currIndex] < max) {
// allocate memory for it
root = new Node(preOrder[currIndex]);
// increment currIndex
currIndex++;
// make left of root as createBST(min, root's data)
root.left = createBST(preOrder, min, root.data);
// make right of root as createBST(root's data, max)
root.right = createBST(preOrder, root.data, max);
}
// return root
return root;
}
public static void main(String[] args) {
// Example 1
int preOrder1[] = new int[] {7, 5, 3, 6, 9};
currIndex = 0;
Node root1 = createBST(preOrder1, Integer.MIN_VALUE, Integer.MAX_VALUE);
inorder(root1);
System.out.println();
// Example 2
int preOrder2[] = new int[] {12, 6, 1, 35, 20};
currIndex = 0;
Node root2 = createBST(preOrder2, Integer.MIN_VALUE, Integer.MAX_VALUE);
inorder(root2);
System.out.println();
}
}3 5 6 7 9 1 6 12 20 35
C++ Code for Construct BST from given Preorder Traversal
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// globally defined currIndex integer
int currIndex = 0;
// function to print the in-order traversal of a binary tree
void inOrder(Node *root) {
if (root != NULL) {
inOrder(root->left);
cout<<root->data<<" ";
inOrder(root->right);
}
}
Node* createBST(int *preOrder, int min, int max, int n) {
if (currIndex >= n) {
return NULL;
}
Node *root = NULL;
// if current element is in between min and max
if (preOrder[currIndex] > min && preOrder[currIndex] < max) {
// allocate memory for it
root = new Node(preOrder[currIndex]);
// increment currIndex
currIndex++;
// make left of root as createBST(min, root's data)
root->left = createBST(preOrder, min, root->data, n);
// make right of root as createBST(root's data, max)
root->right = createBST(preOrder, root->data, max, n);
}
// return root
return root;
}
int main() {
// Example 1
int preOrder1[] = {7, 5, 3, 6, 9};
currIndex = 0;
Node *root1 = createBST(preOrder1, INT_MIN, INT_MAX, sizeof(preOrder1) / sizeof(preOrder1[0]));
inOrder(root1);
cout<<endl;
// Example 2
int preOrder2[] = {12, 6, 1, 35, 20};
currIndex = 0;
Node *root2 = createBST(preOrder2, INT_MIN, INT_MAX, sizeof(preOrder2) / sizeof(preOrder2[0]));
inOrder(root2);
cout<<endl;
return 0;
}3 5 6 7 9 1 6 12 20 35
Iterative Method
Here we use a stack to cut down the recursion and convert the optimal approach to an iterative code.
- The first node is the root of BST, so make the root as the first node and push it to a stack.
- Traverse the pre-order array from index 1(0 based indexing) and for each element, while the current element is greater than the top of stack pop out the top and store it in a variable named temp.
- If the temp is null(that is current element was smaller than stack’s top), make temp as the top of the stack and current element as left of temp and push the current element to the stack.
- Else make the current element as the right of temp and push the current element to the stack.
- Return root.
Time Complexity = O(n)
Space Complexity = O(n)
where n is the size of the pre-order array.
JAVA Code for Construct BST from given Preorder Traversal
import java.util.Stack;
public class ConstructBSTFromGivenPreorderTraversal {
// class representing Node of a Binary Tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to print inorder of a Binary Tree
private static void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
private static Node createBST(int[] preOrder) {
// the first element is the root of BST
Node root = new Node(preOrder[0]);
// create a stack and push root to it
Stack<Node> stack = new Stack<>();
stack.push(root);
// traverse the array from index 1
for (int i = 1; i < preOrder.length; i++) {
// initialize temp as null
Node temp = null;
// while current element is greater than top of stack
// remove top of stack and store it in temp
while (!stack.isEmpty() && preOrder[i] > stack.peek().data) {
temp = stack.pop();
}
// if temp is null
if (temp == null) {
// make temp as top of stack
temp = stack.peek();
// current element is left of temp
temp.left = new Node(preOrder[i]);
// add current element to stack
stack.push(temp.left);
} else {
// current element is right of temp
temp.right = new Node(preOrder[i]);
// add current element to the stack
stack.push(temp.right);
}
}
// return root
return root;
}
public static void main(String[] args) {
// Example 1
int preOrder1[] = new int[] {7, 5, 3, 6, 9};
Node root1 = createBST(preOrder1);
inorder(root1);
System.out.println();
// Example 2
int preOrder2[] = new int[] {12, 6, 1, 35, 20};
Node root2 = createBST(preOrder2);
inorder(root2);
System.out.println();
}
}3 5 6 7 9 1 6 12 20 35
C++ Code for Construct BST from given Preorder Traversal
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to print the in-order traversal of a binary tree
void inOrder(Node *root) {
if (root != NULL) {
inOrder(root->left);
cout<<root->data<<" ";
inOrder(root->right);
}
}
Node* createBST(int *preOrder, int n) {
// the first element is the root of BST
Node *root = new Node(preOrder[0]);
// create a stack and push root to it
stack<Node*> st;
st.push(root);
// traverse the array from index 1
for (int i = 1; i < n; i++) {
// initialize temp as null
Node *temp = NULL;
// while current element is greater than top of stack
// remove top of stack and store it in temp
while (!st.empty() && preOrder[i] > st.top()->data) {
temp = st.top();
st.pop();
}
// if temp is null
if (temp == NULL) {
// make temp as top of stack
temp = st.top();
// current element is left of temp
temp->left = new Node(preOrder[i]);
// add current element to stack
st.push(temp->left);
} else {
// current element is right of temp
temp->right = new Node(preOrder[i]);
// add current element to the stack
st.push(temp->right);
}
}
// return root
return root;
}
int main() {
// Example 1
int preOrder1[] = {7, 5, 3, 6, 9};
Node *root1 = createBST(preOrder1, sizeof(preOrder1) / sizeof(preOrder1[0]));
inOrder(root1);
cout<<endl;
// Example 2
int preOrder2[] = {12, 6, 1, 35, 20};
Node *root2 = createBST(preOrder2, sizeof(preOrder2) / sizeof(preOrder2[0]));
inOrder(root2);
cout<<endl;
return 0;
}3 5 6 7 9 1 6 12 20 35