Table of Contents
Problem Statement
Given a complete Binary Search Tree, write an algorithm to convert it into a Min Heap, which is to convert BST to Min Heap. The Min Heap should be such that the values on the left of a node must be less than the values on the right of that node.
Example
Input

Output
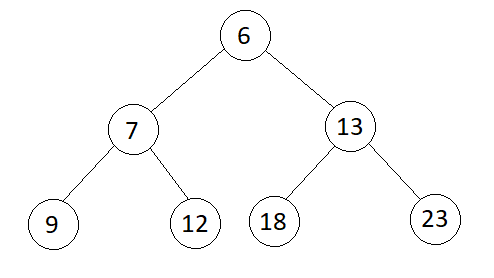
Level Order : 6 7 13 9 12 18 23
Algorithm to convert BST to Min Heap
A Binary Search Tree contains elements such that its’ in-order traversal gives the elements in sorted form. To convert BST to Min Heap we convert the in-order traversal of the Binary Search Tree in pre-order traversal, that is, we store the in-order traversal of the tree in an array and then replace the nodes in pre-order fashion with the in-order output.
This will ensure that the Binary Search Tree converts to a Min Heap and also the Min Heap satisfies the given property, that is, all the nodes in the left sub-tree of a node is smaller than all the nodes in the right sub-tree of that tree.
1. Traverse the BST in in-order traversal and store the traversal in an array or a list. 2. This time traverse the Binary Search Tree in pre-order form. 3. Replace every node with the corresponding value stored in the array or list.
Time Complexity = O(N)
Since we performed in-order and pre-order traversals of the tree which take only O(N) time.
Space Complexity = O(N)
Here we are storing n elements, thus a linear space complexity space solution/.
where N is the total number of nodes in the complete Binary Search Tree.
Explanation
Consider the tree shown in the above example.
Step 1
Traverse the tree in in-order form and store it in an array.
arr[] = {6, 7, 9, 12, 13, 18, 23}
Step 2 & 3
Traverse the tree in pre-order form and replace every node’s value with the corresponding value stored in the array.

As we can see in the figure, the tree is converted into a Min Heap satisfying the given properties.
Code
Java Code to convert BST to Min Heap
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
class ConvertBSTToMinHeap {
// class representing node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to print level order traversal of binary tree
private static void levelOrder(Node root) {
if (root == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node curr = queue.poll();
System.out.print(curr.data + " ");
if (curr.left != null)
queue.add(curr.left);
if (curr.right != null)
queue.add(curr.right);
}
}
// function to store the inorder traversal of tree in a list
private static void storeInOrder(Node root, ArrayList<Integer> inOrder) {
if (root != null) {
storeInOrder(root.left, inOrder);
inOrder.add(root.data);
storeInOrder(root.right, inOrder);
}
}
// function to replace the inorder traversal with pre-order traversal
private static void replaceInOrderWithPreOrder(Node root, ArrayList<Integer> inOrder) {
if (root != null) {
root.data = inOrder.get(0);
inOrder.remove(0);
replaceInOrderWithPreOrder(root.left, inOrder);
replaceInOrderWithPreOrder(root.right, inOrder);
}
}
private static void convertToMinHeap(Node root) {
ArrayList<Integer> inOrderTraversal = new ArrayList<>();
// store the in order traversal of the tree in a list
storeInOrder(root, inOrderTraversal);
// replace the pre order traversal with in order traversal
replaceInOrderWithPreOrder(root, inOrderTraversal);
}
public static void main(String[] args) {
// Example Tree
Node root = new Node(12);
root.left = new Node(7);
root.right = new Node(18);
root.left.left = new Node(6);
root.left.right = new Node(9);
root.right.left = new Node(13);
root.right.right = new Node(23);
convertToMinHeap(root);
levelOrder(root);
System.out.println();
}
}
6 7 13 9 12 18 23
C++ Code to convert BST to Min Heap
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to print level order traversal of binary tree
void levelOrder(Node *root) {
if (root == NULL) {
return;
}
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node *curr = q.front();
q.pop();
cout<<curr->data<<" ";
if (curr->left != NULL)
q.push(curr->left);
if (curr->right != NULL)
q.push(curr->right);
}
}
// function to store the inorder traversal of tree in a list
void storeInOrder(Node *root, vector<int> &inOrderTraversal) {
if (root != NULL) {
storeInOrder(root->left, inOrderTraversal);
inOrderTraversal.push_back(root->data);
storeInOrder(root->right, inOrderTraversal);
}
}
// function to replace the inorder traversal with pre-order traversal
void replaceInOrderWithPreOrder(Node *root, vector<int> &inOrderTraversal) {
if (root != NULL) {
root->data = inOrderTraversal[0];
inOrderTraversal.erase(inOrderTraversal.begin());
replaceInOrderWithPreOrder(root->left, inOrderTraversal);
replaceInOrderWithPreOrder(root->right, inOrderTraversal);
}
}
void convertToMinHeap(Node *root) {
std::vector<int> inOrderTraversal;
// store the in order traversal of the tree in a list
storeInOrder(root, inOrderTraversal);
// replace the pre order traversal with in order traversal
replaceInOrderWithPreOrder(root, inOrderTraversal);
}
int main() {
// Example Tree
Node *root = new Node(12);
root->left = new Node(7);
root->right = new Node(18);
root->left->left = new Node(6);
root->left->right = new Node(9);
root->right->left = new Node(13);
root->right->right = new Node(23);
convertToMinHeap(root);
levelOrder(root);
cout<<endl;
return 0;
}6 7 13 9 12 18 23