Table of Contents
Problem Statement
“Find k-th smallest element in BST (Order Statistics in BST)” problem states that you are given a binary search tree and you need to find the k-th smallest number in the BST. This means if we do an in-order traversal of the binary search tree and store the result in a vector /an array. Then the element at index (k-1) will be the kth smallest if we consider 0 – based indexing.
Example
Input
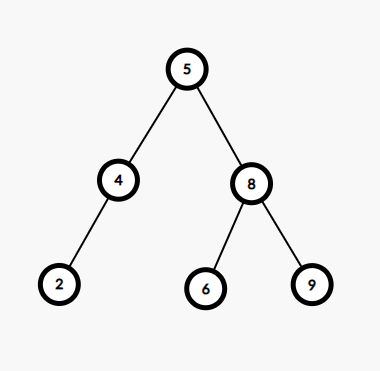
k = 4
6
Explanation: If we do an in-order traversal of the given binary tree we get {2, 4, 5, 6, 8, 9}. So in this, we need to find the 4th smallest element then that is 6. Thus the output is 6.
Approach
Augmented Tree Data Structure
In this approach, we consider that each node stores the element in its left sub-tree. While building the tree we maintain the elements in the left subtree of each node. This fact is used to find the k-th smallest element in the tree. So when we try to find the kth element we check that if the left subtree has more elements than k. Then our k-th smallest element lies in the left sub-tree else it lies in the right sub-tree. And that’s how we find the k-th smallest element in the BST.
Code
C++ code to find k-th smallest element in the BST
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
int leftCnt;
node *left;
node *right;
} ;
node* create(int data){
node * tmp = new node();
tmp->data = data;
tmp->leftCnt = 0;
tmp->left = tmp->right = NULL;
return tmp;
}
node* insert(node* root, int x)
{
if (root == NULL)
return create(x);
// we do the same as done to insert an element in the BST
// but if we insert an element in the left sub-tree
// we increment the count of nodes in left sub-tree as well
if(x<root->data){
root->left = insert(root->left, x);
root->leftCnt++;
}
else if(x>root->data)
root->right = insert(root->right, x);
return root;
}
node* findKthSmallest(node *root, int k)
{
if (!root)
return NULL;
int cnt = root->leftCnt+1;
// current node is the k-th smallest element
if(cnt == k)
return root;
else if(k > cnt)
return findKthSmallest(root->right, k-cnt);
else
return findKthSmallest(root->left, k);
}
int main()
{
node *root = NULL;
int n;cin>>n;
for(int i=0;i<n;i++){
int element;cin>>element;
root = insert(root, element);
}
int k;cin>>k;
node* res = findKthSmallest(root, k);
if(res == NULL)
cout<<"No kth smallest found";
else
cout<<"Kth smallest element is "<<res->data;
}6 5 4 2 8 6 9 4
6
Java code to find k-th smallest element in BST
import java.util.*;
import java.lang.*;
import java.io.*;
class node{
int data;
int leftCnt;
node left;
node right;
}
class Tree{
static node root;
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.leftCnt = 0;
tmp.left = null;
tmp.right = null;
return tmp;
}
static node insert(node root, int x)
{
if (root == null)
return create(x);
// we do the same as done to insert an element in the BST
// but if we insert an element in the left sub-tree
// we increment the count of nodes in left sub-tree as well
if(x<root.data){
root.left = insert(root.left, x);
root.leftCnt++;
}
else if(x>root.data)
root.right = insert(root.right, x);
return root;
}
static node findKthSmallest(node root, int k)
{
if (root == null)
return null;
int cnt = root.leftCnt+1;
// current node is the k-th smallest element
if(cnt == k)
return root;
else if(k > cnt)
return findKthSmallest(root.right, k-cnt);
else
return findKthSmallest(root.left, k);
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i=0;i<n;i++){
int element = sc.nextInt();
root = insert(root, element);
}
int k = sc.nextInt();
node res = findKthSmallest(root, k);
if(res == null)
System.out.println("No kth smallest found");
else
System.out.println("Kth smallest element is "+res.data);
}
}6 5 4 2 8 6 9 4
Kth smallest element is 6
Complexity Analysis
Time Complexity
O(H), in worst case H can be equal to N if we have a skewed tree as input and we need to find the Nth smallest element.
Space Complexity
O(H), here we do not consider the space required by leftCnt to count the number of nodes in the left subtree. We consider that the leftCnt is part of the tree and thus O(H) space is the space required by the recursion.
Inorder Traversal
“Find k-th smallest element in BST (Order Statistics in BST)” can be solved using inorder traversal because the inorder traversal of the Binary Search Tree traverses the nodes in the increasing order. Thus we can keep a count variable. When this count variable becomes equal to k, we know we are at the k-th smallest element in BST.
Code
C++ code to find k-th smallest element in the BST
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
node *left;
node *right;
} ;
node* create(int data){
node * tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
// normally insert the node in BST
node* insert(node* root, int x)
{
if (root == NULL)
return create(x);
if(x<root->data)
root->left = insert(root->left, x);
else if(x>root->data)
root->right = insert(root->right, x);
return root;
}
node* findKthSmallest(node* root, int& k)
{
// base case
if(!root)
return NULL;
node *left = findKthSmallest(root->left, k);
if(left)
return left;
// if current element is kth smallest
if(k==1)
return root;
// if the kth smallest is not found in the left subtree
// search in right subtree
k--;
return findKthSmallest(root->right, k);
}
int main()
{
node *root = NULL;
int n;cin>>n;
for(int i=0;i<n;i++){
int element;cin>>element;
root = insert(root, element);
}
int k;cin>>k;
node* res = findKthSmallest(root, k);
if(res == NULL)
cout<<"No kth smallest found";
else
cout<<"Kth smallest element is "<<res->data;
}
6 5 4 2 8 6 9 4
Kth smallest element is 6
Java Code to find k-th smallest element in the BST
import java.util.*;
import java.lang.*;
import java.io.*;
class node{
int data;
node left;
node right;
}
class Tree{
static node root;
static int count;
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = null;
tmp.right = null;
return tmp;
}
static node insert(node root, int x)
{
if (root == null)
return create(x);
if(x<root.data)
root.left = insert(root.left, x);
else if(x>root.data)
root.right = insert(root.right, x);
return root;
}
static node findKthSmallest(node root, int k)
{
// base case
if(root == null)
return null;
node left = findKthSmallest(root.left, k);
if(left != null)
return left;
count++;
// if current element is kth smallest
if(k==count)
return root;
// if the kth smallest is not found in the left subtree
// search in right subtree
return findKthSmallest(root.right, k);
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i=0;i<n;i++){
int element = sc.nextInt();
root = insert(root, element);
}
int k = sc.nextInt();
count = 0;
node res = findKthSmallest(root, k);
if(res == null)
System.out.println("No kth smallest found");
else
System.out.println("Kth smallest element is "+res.data);
}
}6 5 4 2 8 6 9 4
Kth smallest element is 6
Complexity Analysis
Time Complexity
O(N), because to reach the k-th element we first need to traverse k-1 elements. And thus even if the kth element was the root, we would have to traverse through all the elements of the left subtree.
Space Complexity
O(H), here this space complexity is due to recursion. Even though the whole program has linear space complexity. The algorithm itself runs in O(H) space.