In this problem, we have given a BST and a number k, find the kth smallest element in a BST.
Table of Contents
Examples
Input
tree[] = {5, 3, 6, 2, 4, null, null, 1}
k = 3

Output
3
Input
tree[] = {3, 1, 4, null, 2}
k = 1
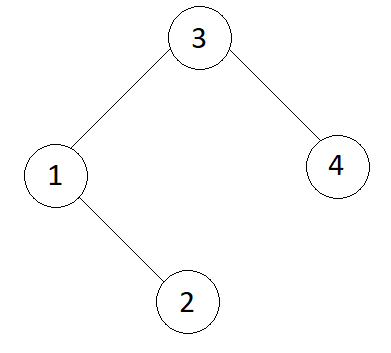
Output
1
Naive Approach for finding Kth Smallest Element in a BST
Do inorder traversal of the BST and store it in an array and return the kth element of the array. As inorder traversal of BST results in a sorted array, so kth element in inorder traversal is the kth smallest element.
- Create a list of integers that stores the inorder traversal of BST.
- Do inorder traversal
- If the root is not null recursively do inorder traversal for the left child.
- Insert the current node’s data to the list.
- Recursively do inorder traversal for the right child.
- In the end, return the element present at the kth position in the list.
JAVA Code
import java.util.ArrayList;
public class KthSmallestInBST {
// Class representing node of BST
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
left = right = null;
}
}
// Function to do in order traversal of BST and store it in array
private static void inorder(Node root, ArrayList<Integer> traversal) {
if (root != null) {
inorder(root.left, traversal);
traversal.add(root.data);
inorder(root.right, traversal);
}
}
private static int kthSmallest(Node root, int k) {
ArrayList<Integer> traversal = new ArrayList<>();
// Do inorder traversal and store in an array
inorder(root, traversal);
// Return the kth element of the array
return traversal.get(k - 1);
}
public static void main(String[] args) {
// Example 1
Node root = new Node(5);
root.left = new Node(3);
root.right = new Node(6);
root.left.left = new Node(2);
root.left.right = new Node(4);
root.left.left.left = new Node(1);
int k = 3;
System.out.println(kthSmallest(root, k));
// Example 2
Node root2 = new Node(3);
root2.left = new Node(1);
root2.right = new Node(4);
root2.left.right = new Node(2);
k = 1;
System.out.println(kthSmallest(root2, k));
}
}C++ Code
#include <bits/stdc++.h>
using namespace std;
// Class representing node of BST
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// Function to do in order traversal of BST and store it in array
void inorder(Node *root, vector<int> &traversal) {
if (root != NULL) {
inorder(root->left, traversal);
traversal.push_back(root->data);
inorder(root->right, traversal);
}
}
int kthSmallest(Node *root, int k) {
vector<int> traversal;
// Do inorder traversal and store in an array
inorder(root, traversal);
// Return the kth element of the array
return traversal[k - 1];
}
int main() {
// Example 1
Node *root = new Node(5);
root->left = new Node(3);
root->right = new Node(6);
root->left->left = new Node(2);
root->left->right = new Node(4);
root->left->left->left = new Node(1);
int k = 3;
cout<<kthSmallest(root, k)<<endl;
// Example 2
Node *root2 = new Node(3);
root2->left = new Node(1);
root2->right = new Node(4);
root2->left->right = new Node(2);
k = 1;
cout<<kthSmallest(root2, k)<<endl;
return 0;
}3 1
Complexity Analysis of finding Kth Smallest Element in a BST
Time Complexity = O(n)
Space Complexity = O(n)
where n is the number of nodes in BST.
Optimal Approach for finding Kth Smallest Element in a BST
The better approach to solve this problem is to use augmented BST, that is, we store the count of nodes in the left subtree with every node. Let this be represented as leftCount.
- Start from the root of the tree.
- If the current node’s leftCount is (k – 1), this is the kth smallest node, return the node.
- If the current node’s leftCount is less than (k – 1), search in the right subtree and update k as (k – leftCount – 1).
- Else if the current node’s leftCount is greater than (k – 1), search in the left subtree.
Time Complexity = O(h), where h is the height of BST
Also, insert in BST is modifies as,
If the new node is to be inserted in the left subtree of the current node, then increment the value of leftCount of a current node by 1, else insert as we do in a normal BST.
JAVA Code
public class KthSmallestInBST {
// class representing Node of augmented BST
static class Node {
int data;
int leftCount;
Node left, right;
public Node(int data) {
this.data = data;
this.leftCount = 0;
left = right = null;
}
}
private static Node insert(Node root, int value) {
// Base Case
if (root == null) {
return new Node(value);
}
// If the new node is to be inserted in the left subtree, increment the leftCount
// of the current node by 1
if (value < root.data) {
root.left = insert(root.left, value);
root.leftCount++;
} else if (value > root.data) {
root.right = insert(root.right, value);
}
return root;
}
private static int kthSmallest(Node root, int k) {
// kth smallest element does not exist
if (root == null) {
return -1;
}
// If lefCount is equals to k - 1, this is the kth smallest element
if (root.leftCount == k - 1) {
return root.data;
} else if (root.leftCount > k - 1) {
// If leftCount is greater than k - 1, search in the left subtree
return kthSmallest(root.left, k);
} else {
// Else search in the right subtree
return kthSmallest(root.right, k - root.leftCount - 1);
}
}
public static void main(String[] args) {
// Example 1
Node root = null;
root = insert(root, 5);
root = insert(root, 3);
root = insert(root, 6);
root = insert(root, 2);
root = insert(root, 4);
root = insert(root, 1);
int k = 3;
System.out.println(kthSmallest(root, k));
// Example 2
Node root2 = null;
root2 = insert(root2, 3);
root2 = insert(root2, 1);
root2 = insert(root2, 4);
root2 = insert(root2, 2);
k = 1;
System.out.println(kthSmallest(root2, k));
}
}C++ Code
#include <bits/stdc++.h>
using namespace std;
// class representing Node of augmented BST
class Node {
public:
int data;
int leftCount;
Node *left;
Node *right;
Node(int d) {
data = d;
leftCount = 0;
left = right = NULL;
}
};
Node* insert(Node *root, int value) {
// Base Case
if (root == NULL) {
return new Node(value);
}
// If the new node is to be inserted in the left subtree, increment the
// leftCount of the current node by 1
if (value < root->data) {
root->left = insert(root->left, value);
root->leftCount++;
} else if (value > root->data) {
root->right = insert(root->right, value);
}
return root;
}
int kthSmallest(Node* root, int k) {
// kth smallest element does not exist
if (root == NULL) {
return -1;
}
// If lefCount is equals to k - 1, this is the kth smallest element
if (root->leftCount == k - 1) {
return root->data;
} else if (root->leftCount > k - 1) {
// If leftCount is greater than k - 1, search in the left subtree
return kthSmallest(root->left, k);
} else {
// Else search in the right subtree
return kthSmallest(root->right, k - root->leftCount - 1);
}
}
int main() {
// Example 1
Node *root = NULL;
root = insert(root, 5);
root = insert(root, 3);
root = insert(root, 6);
root = insert(root, 2);
root = insert(root, 4);
root = insert(root, 1);
int k = 3;
cout<<kthSmallest(root, k)<<endl;
// Example 2
Node *root2 = NULL;
root2 = insert(root2, 3);
root2 = insert(root2, 1);
root2 = insert(root2, 4);
root2 = insert(root2, 2);
k = 1;
cout<<kthSmallest(root2, k)<<endl;
return 0;
}3 1