Table of Contents
Problem Statement
The problem “Merge two BSTs with limited extra space” states that you are given two binary search tree(BST) and you need to print the elements from both the trees in sorted order. That is in such an order that it seems that elements are from a single BST.
Example
Input
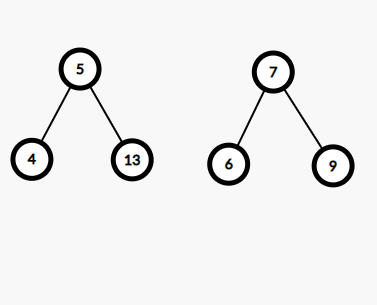
Output
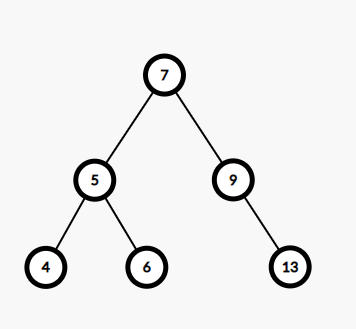
4 5 6 7 9 13
Explanation: The new tree formed by merging both the input trees is shown in the image. The inorder traversal of the resultant tree gives the output.
Approach to Merge two BSTs with limited extra space
The problem “Merge two BSTs with limited extra space” asks us to print the inorder traversal of the merged tree. The merged tree will be formed by merging of the given two trees. Thus we will try to merge the given trees. But if we were to merge the trees then this requires much overhead. Instead of merging directly, we can think of some other way around. Since we only need to print the values of nodes in both the given trees in sorted form.
For solving this we will try to run iterative inorder traversal of the binary search tree over both the trees simultaneously. This can be done if we run inorder traversal. And compare the value on both the nodes in the inorder traversal. We will then print the smaller of the two and push the larger node in the stack( stack used during the iterative inorder traversal). Whenever we are done with any one of the trees, we will simply run inorder traversal over the tree with nodes remaining.
Code
C++ code to Merge two BSTs with limited extra space
#include <bits/stdc++.h>
using namespace std;
struct node
{
int data;
node *left;
node *right;
};
// returns a new node with supplied data
node* create(int data)
{
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void inorder(node *root)
{
if(root){
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
void merge(node *root1, node *root2)
{
stack<node*> s1;node* cur1 = root1;
stack<node*> s2;node* cur2 = root2;
//if first tree is empty, print second tree
if(!root1){
inorder(root2);
return;
}
// if second tree is empty, print first tree
if(!root2){
inorder(root2);
return;
}
// print the nodes which are not yet visited or visited but not printed
while(cur1 != NULL || !s1.empty() || cur2 != NULL || !s2.empty())
{
// iterative inorder
if(cur1 != NULL || cur2 != NULL)
{
// Reach the leftmost node of both BSTs and push ancestors of
// leftmost nodes to stack s1 and s2 respectively
if(cur1 != NULL)
{
s1.push(cur1);
cur1 = cur1->left;
}
if (cur2 != NULL)
{
s2.push(cur2);
cur2 = cur2->left;
}
}
else
{
// if anyone of the tree's current node becomes Null
// then we need to check if stack is empty
if(s1.empty())
{
while(!s2.empty())
{
cur2 = s2.top();s2.pop();
cur2->left = NULL;
inorder(cur2);
}
return;
}
if(s2.empty())
{
while(!s1.empty())
{
cur1 = s1.top();s1.pop();
cur1->left = NULL;
inorder(cur1);
}
return;
}
// compare elements at the top of both stacks
cur1 = s1.top();s1.pop();
cur2 = s2.top();s2.pop();
// print the smaller of the two and push the larger element into the corresponding stack
if(cur1->data < cur2->data)
{
cout<<cur1->data<<" ";
cur1 = cur1->right;
s2.push(cur2);
cur2 = NULL;
}
else
{
cout<<cur2->data<<" ";
cur2 = cur2->right;
s1.push(cur1);
cur1 = NULL;
}
}
}
}
int main()
{
node *root1 = NULL, *root2 = NULL;
//first tree
root1 = create(5);
root1->left = create(4);
root1->right = create(13);
//second tree
root2 = create(7);
root2->left = create(6);
root2->right = create(9);
// Print sorted nodes of both trees
merge(root1, root2);
return 0;
}
4 5 6 7 9 13
Java code to Merge two BSTs with limited extra space
import java.util.*;
import java.lang.*;
import java.io.*;
class node{
int data;
node left;
node right;
}
class Tree{
static node root;
static int count;
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = null;
tmp.right = null;
return tmp;
}
static void inorder(node root)
{
if(root != null){
inorder(root.left);
System.out.print(root.data+" ");
inorder(root.right);
}
}
static void merge(node root1, node root2)
{
Stack<node> s1 = new Stack<>();node cur1 = root1;
Stack<node> s2 = new Stack<>();node cur2 = root2;
//if first tree is empty, print second tree
if(root1 == null){
inorder(root2);
return;
}
// if second tree is empty, print first tree
if(root2 == null){
inorder(root1);
return;
}
// print the nodes which are not yet visited or visited but not printed
while(cur1 != null || s1.empty() == false || cur2 != null || s2.empty() == false)
{
if(cur1 != null || cur2 != null)
{
// Reach the leftmost node of both BSTs and push ancestors of
// leftmost nodes to stack s1 and s2 respectively
if(cur1 != null)
{
s1.push(cur1);
cur1 = cur1.left;
}
if (cur2 != null)
{
s2.push(cur2);
cur2 = cur2.left;
}
}
else
{
// if anyone of the tree's current node becomes Null
// then we need to check if stack is empty
if(s1.empty() == true)
{
while (s2.empty() == false)
{
cur2 = s2.pop();
cur2.left = null;
inorder(cur2);
}
return ;
}
if(s2.empty() == true)
{
while (s1.empty() == false)
{
cur1 = s1.pop();
cur1.left = null;
inorder(cur1);
}
return ;
}
// compare elements at the top of both stacks
cur1 = s1.pop();
cur2 = s2.pop();
// print the smaller of the two and push the larger element into the corresponding stack
if (cur1.data < cur2.data)
{
System.out.print(cur1.data+" ");
cur1 = cur1.right;
s2.push(cur2);
cur2 = null;
}
else
{
System.out.print(cur2.data+" ");
cur2 = cur2.right;
s1.push(cur1);
cur1 = null;
}
}
}
}
public static void main(String[] args)
{
node root1 = null;
node root2 = null;
//first tree
root1 = create(5);
root1.left = create(4);
root1.right = create(13);
//second tree
root2 = create(7);
root2.left = create(6);
root2.right = create(9);
// Print sorted nodes of both trees
merge(root1, root2);
}
}
4 5 6 7 9 13
Complexity Analysis
Time Complexity
O(N+M), because we have done simultaneous inorder traversal over both the trees. During the inorder traversal, we went over the nodes from both the trees and thus a linear time complexity.
Space Complexity
O(N+M), more formally space complexity will be the sum of the height of both trees. But in the worst case, the input can be skewed trees and in that case, height will be equal to the number of nodes in trees.