Morris Inorder Traversal

Difficulty Level Medium
Tree Tree TraversalViews 2749

We can traverse a tree in the inorder fashion iteratively, using stack, but it consumes space. So, in this problem, we are going to traverse a tree without the linear space being used. This concept is called Morris Inorder Traversal or Threading in Binary trees.

Example

          2

       /      \

     1           3

  /      \

4          5
4 1 5 2 3
       3

    /      \

  1          4
            
          /      \
 
        2          5
1 3 2 4 5

Approach

The idea is: we can traverse the tree without the space of a stack (or the auxiliary space of recursion) if we do not lose the address of any node we visited earlier without storing them in the memory. This approach is called Morris Inorder Traversal.

But without any space allowed, how can one store the addresses of nodes? The idea is to change the structure of the tree in such a way, that after visiting some particular nodes of one subtree from the root node, we can get back to the root node to process its other subtree. Say we visited the left subtree completely, and add a pointer from some node of the left subtree to the root again. Now, we can process the right subtree by coming back to the original root. In Morris Inorder Traversal, we link the inorder predecessor of a root(in its left subtree) to itself.

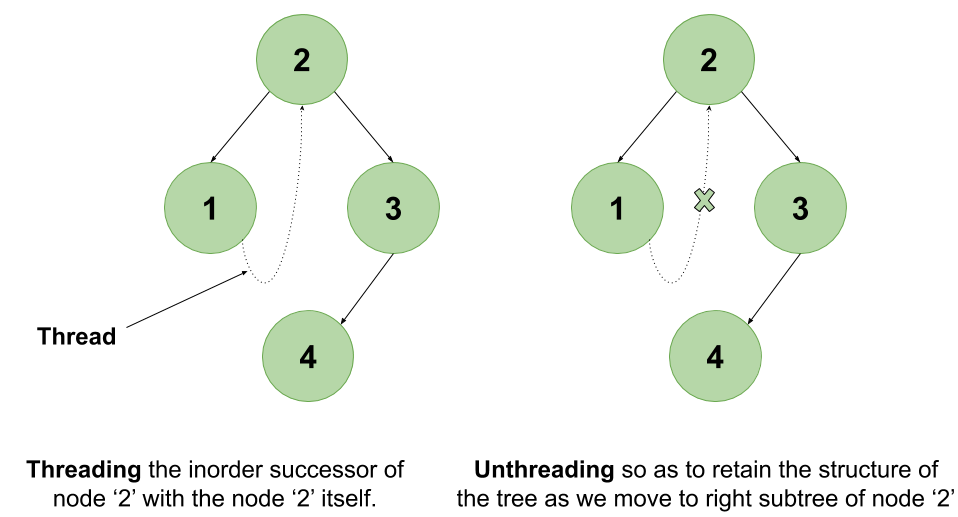
Morris Inorder Traversal C++ Tutorial

This process of adding pointers (threads) from the inorder predecessor to root is called threading. Again, we don’t want to disturb the structure of the tree, so we will design an algorithm that automatically deletes the links and unthreads the tree to retain its original structure.

Algorithm

  1. Initialize the current node as root of the tree.
  2. Keep iterating till we reach the condition where the current node becomes NULL. 
    • If the left subtree of the current root is NULL :
        • We can now print the root and move to the right subtree, so currentNode = currentNode->right.
    • If the left subtree of the current root is  NOT NULL :
        • In this case, we unthread/thread the rightmost node in the left subtree(inorder predecessor) of the current node to itself
            • temp = currentNode->left;
            • While temp->right is NOT NULL or temp is NOT currentNode
              • temp = temp->right
        • If temp->right is NULL:
            • remove threading as temp->right = NULL
            • process the right subtree, currentNode = currentNode->right
        • If temp->right is NOT NULL:
            • thread this node as temp->right = currentNode
            • Process the left subtree now, currentNode = currentNode->left

Implementation of Morris Inorder Traversal

C++ Program

#include <bits/stdc++.h>

using namespace std;

struct treeNode
{
    int value;
    treeNode *left , *right;
    treeNode(int x)
    {
        value = x;
        left = NULL;
        right = NULL;
    }
};


void morrisInorder(treeNode* &root)
{
    treeNode* currentNode = root;
    while(currentNode != NULL)
    {
        if(currentNode->left == NULL)
        {
            cout << currentNode->value << " ";
            currentNode = currentNode->right;
        }
        else
        {
            treeNode* temp = currentNode->left;
            while((temp->right != NULL) && (temp->right != currentNode))
                temp = temp->right;

            if(temp->right == NULL)
            {
                temp->right = currentNode;
                //threading
                currentNode = currentNode->left;
            }
            else
            {
                cout << currentNode->value << " ";
                temp->right = NULL;
                //unthreading
                currentNode = currentNode->right;
            }
        }
    }
}

int main()
{
    treeNode* root = new treeNode(2);
    root->left = new treeNode(1);
    root->right = new treeNode(3);
    root->left->left = new treeNode(4);
    root->left->right = new treeNode(5);

    morrisInorder(root);
    return 0;
}

4 1 5 2 3

Java Program

class treeNode
{
    int value;
    treeNode left, right;

    public treeNode(int x)
    {
        value = x;
        left = right = null;
    }
}

class BinaryTree
{
    treeNode root;
    void MorrisInorder()
    {
        treeNode currentNode = root;

        while(currentNode != null)
        {
            if(currentNode.left == null)
            {
                System.out.print(currentNode.value + " ");
                currentNode = currentNode.right;
            }
            else
            {
                treeNode temp = currentNode;
                while(temp.right != null && temp.right != currentNode)
                    temp = temp.right;

                if(temp.right == null)
                {
                    temp.right = currentNode;
                    currentNode = currentNode.left;
                }
                else
                {
                    temp.right = null;
                    System.out.print(currentNode.value + " ");
                    currentNode = currentNode.right;
                }
            }
        }

    }

    public static void main(String args[])
    {
        BinaryTree tree = new BinaryTree();
        tree.root = new treeNode(2);
        tree.root.left = new treeNode(1);
        tree.root.left.left = new treeNode(4);
        tree.root.left.right = new treeNode(5);
        tree.root.right = new treeNode(3);
        tree.MorrisInorder();
    }
}

4 1 5 2 3

Complexity Analysis of Morris Inorder Traversal

Time Complexity

O(N), where N is the number of nodes in the tree. It’s certain that we visit every node exactly 2 times, as they all go through the process of threading and unthreading. But, the time complexity remains linear.

Space Complexity

O(1), as we use constant space for declaring some variables. But, no other auxiliary space is used for any purpose. That’s what Morris Inorder Traversal promises about.

Translate »