Path Sum

What is Path Sum Problem?

In the Path Sum problem, we have given a binary tree and an integer SUM. We have to find if any path from the root to leaf has a sum equal to the SUM. Path sum is defined as the sum of all the nodes present in root from root to any leaf node. Here leaf denotes the node with no child. Let’s see the first input-output format of the problem.

Note:  Here we have a predefined Binary Tree whose structure definition is:

Structure definition of  Tree Node used in Path Sum

struct TreeNode {
/*data of the node*/
int val;
/*left pointer*/
TreeNode *left;
/*right pointer*/
TreeNode *right;
/*assign node left and right pointer null and data of node 0*/
TreeNode() : val(0), left(nullptr), right(nullptr) {}
/*assign x as the data of the node*/
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

Input Format

We have given root of the tree which is pre-constructed and SUM value.

Output Format

Print in single-line “YES” if we found any path with sum of those all nodes weight equal to SUM otherwise print “NO”.

Constraints

• root never null it always denotes to the first node of the binary tree.
• 1<=SUM<=100000
• 1<=root->val<=10000

Let us see one example for understanding.

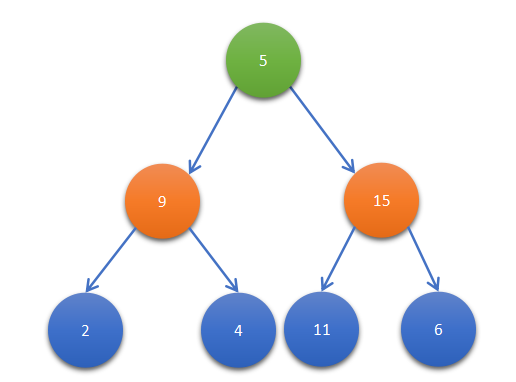
Here we have given root denoting the root of the above tree. Here we have given a sum 18. Now, we start from the root and subtract the value of the root node from it. Now we pass the sum(18-5 = 13) to the left and right subtree of the root node(5). Here we again follow the same step and subtract the node value and pass it to the left and right subtrees. Here at node 2 the sum is 4, at node 4 the sum is 4, for 11 and 6 the sum is negative. Hence we got one leaf node whose value equal to the sum at that node. Hence we say the path from leaf node 4 to root is our answer. In this case, we print “YES”.

Sample Output:
YES

Implementation For Path Sum

/*C++ Implementation of "   Path Sum".*/ 
#include<bits/stdc++.h> 
using namespace std; 
/*tree node structure defination*/
struct TreeNode 
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
/*function return 1 if there is any root to leaf path whose sum equal to given sum value.*/
int check_path_sum(TreeNode * root, int sum)
{
    /*if root is null then return 0*/
    if(!root)
    {
        return 0;
    } 
    /*if leaf node and sum are equal then return 1.*/
    if(!root->left && !root->right && (sum==root->val))
    {
        return 1;
    }     
    /*substract the root value from the sum and pass the sum value to the lefta nd right subtrees.*/
    if(check_path_sum(root->left,sum-root->val) || check_path_sum(root->right,sum-root->val))
    {
        return 1;
    }    
    return 0;
}
int main() 
{
    /*create tree.*/
    TreeNode *ROOT = new TreeNode(5);
    ROOT->left = new TreeNode(9);
    ROOT->right = new TreeNode(15);
    ROOT->left->left = new TreeNode(2);
    ROOT->left->right = new TreeNode(4);
    ROOT->right->left = new TreeNode(11);
    ROOT->right->right = new TreeNode(6);
    /*sum value*/
    int sum=18;
    /*find if there is path or not using function.*/
    int res = check_path_sum(ROOT,sum);
    /*print the answer.*/
    if(res==1)
    {
        cout<<"YES"<<endl;
    }
    else
    {
        cout<<"NO"<<endl;
    }
    return 0;
}

YES

Time Complexity

O(N) where N is the number of nodes present in the given binary tree. Here we just visit each and every node just one’s so our time complexity will be linear.

Space Complexity

O(1) because we don’t use any extra space for the calculation. Here we just visit every node and change the sum value for each node.

Reference  reference2