Table of Contents
Problem Statement
The problem “Range LCM Queries” states that you have an integer array and q number of queries. Each query contains the (left, right) as a range. The given task is to find out the LCM(left, right), i.e, LCM of all the number that comes in the range of left and right inclusively.
Example
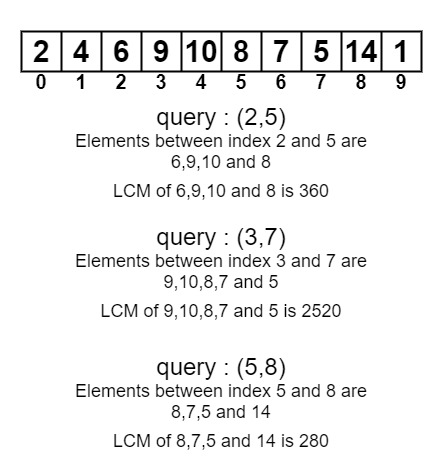
arr[] = {2, 4, 6, 9, 10, 8, 7, 5, 14, 1};
Query: {(2, 5), (3, 7), (5, 8)}360 2520 280
Explanation
for (2,5) the LCM of 6,9,10 and 8 is 360
Now again for the next query i.e., (3,7), LCM of 9,10,8,7 and 5 is 2520
and at last for (5,8) LCM of 8,7,5 and 14 will be 280
Algorithm
- Declare two of the arrays.
- Build a segment tree by recursively calling the functions for the left child and the right child.
- Get the LCM for the left child node and the right child node.
- To get the LCM of a number, divide the product of the left child and right child by their GCD.
- For each query as left and the right, check if the range is not valid then return 1, else check if the left is less than the starting value of the node and the right is greater than the value of the ending node, then return the current value node of the tree.
- If any of the above conditions are not true, else recursively call the function to get the left node lcm and the right node lcm and then call the lcm function to get the LCM of these numbers.
Explanation
Given an integer array and some query with left and right range. Find out the LCM of all the numbers within the range inclusively. To find out the lcm implement the formula as LCM of arr[left, left + 1, ……., right-1, right], but in this, we will be using a tree. We are going to build a segment tree. We will check if there is only one value in an array, then insert that particular value in the node of the tree. Else, we are going to split the array in half and start building the tree, for the left child node. Then pass the values as 2 * node for left node, and for right child node, 2 * node + 1 and get these value’s LCM by passing it into the getLCM function. And get the LCM of these two child nodes and store that returned value at the node position of the tree.
In the LCM function, we are going to find the greatest common divisor of that left and right node values. Then we will return the product of the division of the product of the left and right nodes and the greatest common divisor of the left and right node.
For each query we will get as left and right position, we will double-check the validity of the range if the end value is less than the left or the start value is greater than right, then return 1, it is an invalid question. Else, we will check the validity if left and right is less equal to and greater than equal to start and end respectively, then return the value of the tree at the node. Get the left child value and right child value and get the LCM of these two values and return this value.
Code
C++ code for Range LCM Queries
#include<iostream>
using namespace std;
#define MAX 1000
int tree[4*MAX];
int arr[MAX];
int GCD(int a, int b)
{
if (a == 0)
return b;
return GCD(b%a, a);
}
int getLCM(int a, int b)
{
return a*b/GCD(a,b);
}
int solveQuery(int node, int start, int end, int left, int right)
{
if (end < left || start > right)
return 1;
if (left<=start && right >=end)
return tree[node];
int mid = (start+end)/2;
int leftChildgetLCM = solveQuery(2*node, start, mid, left, right);
int rightChildgetLCM = solveQuery(2*node+1, mid+1, end, left, right);
return getLCM(leftChildgetLCM, rightChildgetLCM);
}
void buildTree(int node, int start, int end)
{
if (start==end)
{
tree[node] = arr[start];
return;
}
int mid = (start+end)/2;
buildTree(2*node, start, mid);
buildTree(2*node+1, mid+1, end);
int leftChildgetLCM = tree[2*node];
int rightChildgetLCM = tree[2*node+1];
tree[node] = getLCM(leftChildgetLCM, rightChildgetLCM);
}
int main()
{
arr[0] = 2;
arr[1] = 4;
arr[2] = 6;
arr[3] = 9;
arr[4] = 10;
arr[5] = 8;
arr[6] = 7;
arr[7] = 5;
arr[8] = 14;
arr[9] = 1;
buildTree(1, 0, 9);
cout << solveQuery(1, 0, 9, 2, 5) << endl;
cout << solveQuery(1, 0, 9, 3, 7) << endl;
cout << solveQuery(1, 0, 9, 5, 8) << endl;
return 0;
}
360 2520 280
Java code for Range LCM Queries
class LCMQueries
{
private static final int MAX = 1000;
private static int tree[] = new int[4 * MAX];
private static int arr[] = new int[MAX];
static int GCD(int a, int b)
{
if (a == 0)
{
return b;
}
return GCD(b % a, a);
}
static int getLCM(int a, int b)
{
return a * b / GCD(a, b);
}
static void buildTree(int node, int start, int end)
{
if (start == end)
{
tree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
buildTree(2 * node, start, mid);
buildTree(2 * node + 1, mid + 1, end);
int leftChildLCM = tree[2 * node];
int rightChildLCM = tree[2 * node + 1];
tree[node] = getLCM(leftChildLCM, rightChildLCM);
}
static int solveQuery(int node, int start,
int end, int left, int right)
{
if (end < left || start > right)
{
return 1;
}
if (left <= start && right >= end)
{
return tree[node];
}
int mid = (start + end) / 2;
int leftChildLCM = solveQuery(2 * node, start, mid, left, right);
int rightChildLCM = solveQuery(2 * node + 1, mid + 1, end, left, right);
return getLCM(leftChildLCM, rightChildLCM);
}
public static void main(String[] args)
{
arr[0] = 2;
arr[1] = 4;
arr[2] = 6;
arr[3] = 9;
arr[4] = 10;
arr[5] = 8;
arr[6] = 7;
arr[7] = 5;
arr[8] = 14;
arr[9] = 1;
buildTree(1, 0, 9);
System.out.println(solveQuery(1, 0, 9, 2, 5));
System.out.println(solveQuery(1, 0, 9, 3, 7));
System.out.println(solveQuery(1, 0, 9, 5, 8));
}
}
360 2520 280
Complexity Analysis
Time Complexity
O(Log N * Log n) where “N” is the number of elements in the array. The other log n denotes the time required for finding the LCM. This time complexity is for each query. The total time complexity is O(N + Q*Log N*log n), this is because O(N) time is required to build the tree and then to answer the queries.
Space Complexity
O(N) where “N” is the number of elements in the array. This space is required for storing the segment tree.