The problem “Write Code to Determine if Two Trees are Identical” states that you are given two binary trees. find out if they are identical or not? Here, identical tree means that both the binary trees have the same node value with the same arrangement of nodes.
Table of Contents
Example
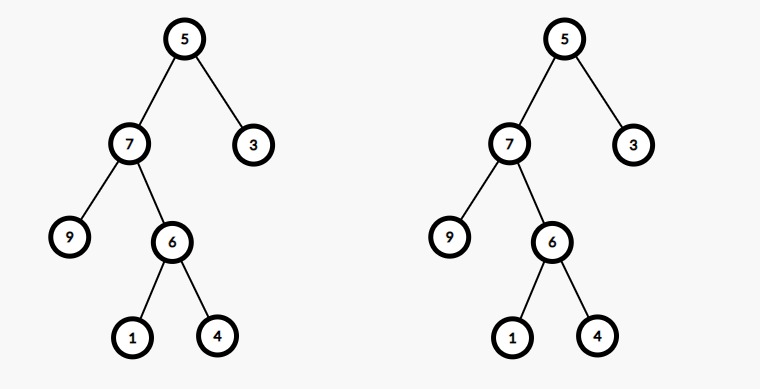
Both trees are identical.
Explanation
Both the trees have the nodes with same value. Also, they have same node arrangement. Thus both the trees are identical.
Approach
A binary tree has only two children for each of the nodes. Now we are given two roots of the binary tree, and we need to check if both the trees are identical. We call two trees are identical if they have the same arrangement of nodes. By the same arrangement, we mean that if some node is in the left direction of some node. They need to be in the same arrangement in the other tree. If both the trees have the same arrangement, they need to have the same value for each of the corresponding nodes in both the trees.
Now we know what trees are called identical. So now we will try to figure out a way to check if two given trees are identical. The method is simple. We need to traverse the trees. while traversing the tree, we keep on checking if the current node of the first tree is the same as that of the second tree. If they differ, then they are not identical. Even if they have some different arrangements. Or if one of the trees had extra nodes as compared to the other one. Then too, we can figure that out by the same method. because if some tree had an extra node, then the other tree will have NULL value at that position. This will result in non-identical trees. So that is how we write code to determine if two trees are identical.
Code
C++ Code to Determine if Two Trees are Identical
#include<bits/stdc++.h>
using namespace std;
struct node {
int data;
node *left, *right;
};
bool identicalTree(node* root1, node* root2){
if(root1 && root2) // if both current nodes are not null
{
if(root1->data == root2->data // both of the current nodes should have same value
&& identicalTree(root1->left, root2->left) // the left subtree of both the trees should also be identical
&& identicalTree(root1->right, root2->right)) // the right subtree of both the trees should also be identical
return true;
return false;
}
else if(!root1 && !root2) // if both tree have current nodes as null nodes
return true;
return false;
}
node* create(int data){
node* tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
int main()
{
node* root1 = create(5);
root1->left = create(7);
root1->right = create(3);
root1->left->left = create(9);
root1->left->right = create(6);
root1->left->right->left = create(1);
root1->left->right->right = create(4);
node* root2 = create(5);
root2->left = create(7);
root2->right = create(3);
root2->left->left = create(9);
root2->left->right = create(6);
root2->left->right->left = create(1);
root2->left->right->right = create(4);
cout<<(identicalTree(root1, root2) ? "Yes" : "No");
}
Yes
Java code to Determine if Two Trees are Identical
import java.util.*;
class node{
int data;
node left, right;
}
class Main{
static boolean identicalTree(node root1, node root2){
if(root1 != null && root2 != null) // if both current nodes are not null
{
if(root1.data == root2.data // both of the current nodes should have same value
&& identicalTree(root1.left, root2.left) // the left subtree of both the trees should also be identical
&& identicalTree(root1.right, root2.right)) // the right subtree of both the trees should also be identical
return true;
return false;
}
else if(root1 == null && root2 == null) // if both tree have current nodes as null nodes
return true;
return false;
}
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = tmp.right = null;
return tmp;
}
public static void main(String[] args){
node root1 = create(5);
root1.left = create(7);
root1.right = create(3);
root1.left.left = create(9);
root1.left.right = create(6);
root1.left.right.left = create(1);
root1.left.right.right = create(4);
node root2 = create(5);
root2.left = create(7);
root2.right = create(3);
root2.left.left = create(9);
root2.left.right = create(6);
root2.left.right.left = create(1);
root2.left.right.right = create(4);
System.out.print(identicalTree(root1, root2) ? "Yes" : "No");
}
}Yes
Complexity Analysis
Time complexity
O(N), where N denotes the minimum number of nodes in both of the trees. Since we have traversed the nodes in the trees. If they had same number of nodes, then the minimum value is same as that of both the nodes. But if they had a different number of nodes, we have to traverse the minimum number of nodes in the worst case.
Space Complexity
O(H), because if we consider the space required for the compiler stack. Then the space required is the same as that taken by the compiler.