Can Make Arithmetic Progression From Sequence Leetcode Solution

Problem statement

In the problem ” Can Make Arithmetic Progression From Sequence” we are given an array, now we need to answer if it is possible to generate an Arithmetic Progression by rearranging the sequence.

Example

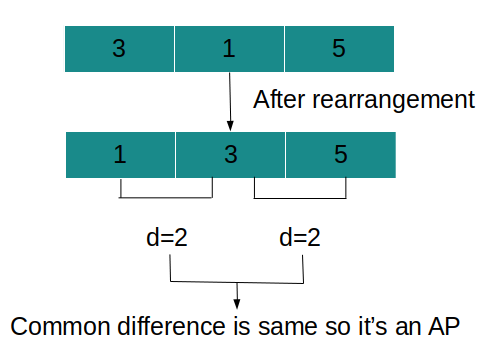
arr = [3,1,5]

true

Explanation: We can rearrange the array as{1,3,5} which forms an arithmetic progression with a common difference as 2, so the output is true.

Approach for Can Make Arithmetic Progression From Sequence Leetcode Solution

An arithmetic series is a series in which the difference between the adjacent number is constant. A very basic approach will be to sort the array and check the difference between adjacent elements, If the difference is the same for all the consecutive pairs then it is an arithmetic progression otherwise it’s not an arithmetic progression.

The time complexity for sorting is nlogn. We can improve the time complexity by creating a lookup table for the array.

The nth term of an AP is= a+(n-1)*d, where a is the first element of the series, n is the number of elements and d is a common difference.

the minimum element of an AP is= a and

the maximum element of an AP is= a+(n-1)*d so

d=(maximum-minimum)/(n-1).

1. We will find the minimum and maximum elements of the array. Using it we can calculate d (common difference).
2. Make a lookup table for the array.
3. Now we know the first element and common difference.
4. We will check if all the n elements of the arithmetic series formed by a and d are present in the lookup table.
5. If all elements are present in the lookup table then we can make the arithmetic progression from the sequence else we can’t make the arithmetic progression from the sequence.

Implementation

C++ code for Can Make Arithmetic Progression From Sequence

#include <bits/stdc++.h> 
using namespace std; 
  bool canMakeArithmeticProgression(vector<int>& arr) {
  unordered_set<int> seen;
  int mi = INT_MAX, mx = INT_MIN, n = arr.size();
        for (int a : arr) {
            mi = min(mi, a);
            mx = max(mx, a);
            seen.insert(a);
        }
        int diff = mx - mi;
        if (diff % (n - 1) != 0) {
            return false;
        }
        diff /= n - 1;
        while (--n > 0) {
            if (seen.find(mi)==seen.end()) {
                return false;
            }
            mi += diff;
        }
        return true;
    }
int main() 
{ 
 vector<int> arr = {3,5,1}; 
 cout <<boolalpha;   
 cout<<canMakeArithmeticProgression(arr)<<endl; 
 return 0;
}

true

Java code for Can Make Arithmetic Progression From Sequence

import java.util.*; 
public class Tutorialcup {
 public static boolean canMakeArithmeticProgression(int[] arr) {
        Set<Integer> seen = new HashSet<>();
        int mi = Integer.MAX_VALUE, mx = Integer.MIN_VALUE, n = arr.length;
        for (int a : arr) {
            mi = Math.min(mi, a);
            mx = Math.max(mx, a);
            seen.add(a);
        }
        int diff = mx - mi;
        if (diff % (n - 1) != 0) {
            return false;
        }
        diff /= n - 1;
        while (--n > 0) {
            if (!seen.contains(mi)) {
                return false;
            }
            mi += diff;
        }
        return true;
    }
  public static void main(String[] args) {
    int [] arr = {3,5,1}; 
    System.out.println( canMakeArithmeticProgression(arr));
  }
}

true

Complexity Analysis of Can Make Arithmetic Progression From Sequence Leetcode Solution

Time complexity

The time complexity of the above code is O(n) because we are traversing the array to create a lookup table and checking if all elements of the arithmetic series are present in the lookup table. Here n is the size of the input array.

Space complexity

The space complexity of the above code is O(n) because we are creating a lookup table for the array. Here n is the size of the input array.

References