Champagne Tower LeetCode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Google Samsung UberViews 3095

Problem Statement

Champagne Tower LeetCode Solution – We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row.  Each glass holds one cup of champagne.

Then, some champagne is poured into the first glass at the top.  When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it.  When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on.  (A glass at the bottom row has its excess champagne fall on the floor.)

For example, after one cup of champagne is poured, the top most glass is full.  After two cups of champagne are poured, the two glasses on the second row are half full.  After three cups of champagne are poured, those two cups become full – there are 3 full glasses total now.  After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.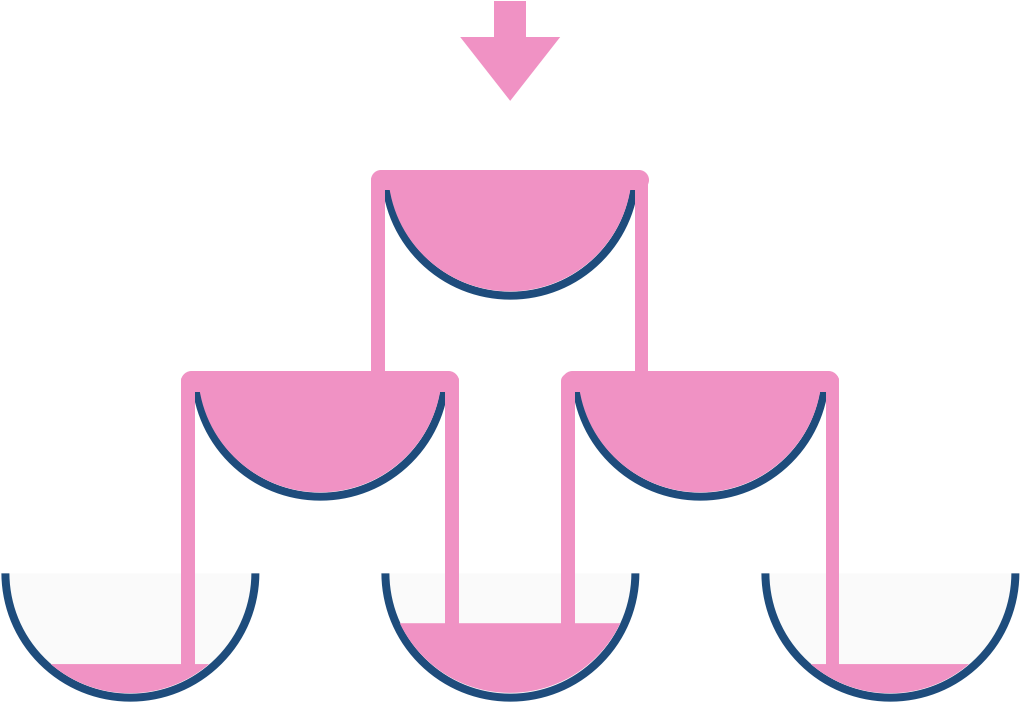Champagne Tower LeetCode Solution

Input: poured = 1, query_row = 1, query_glass = 1
Output: 0.00000
Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.

Explanation

We will be using the concept DP here.

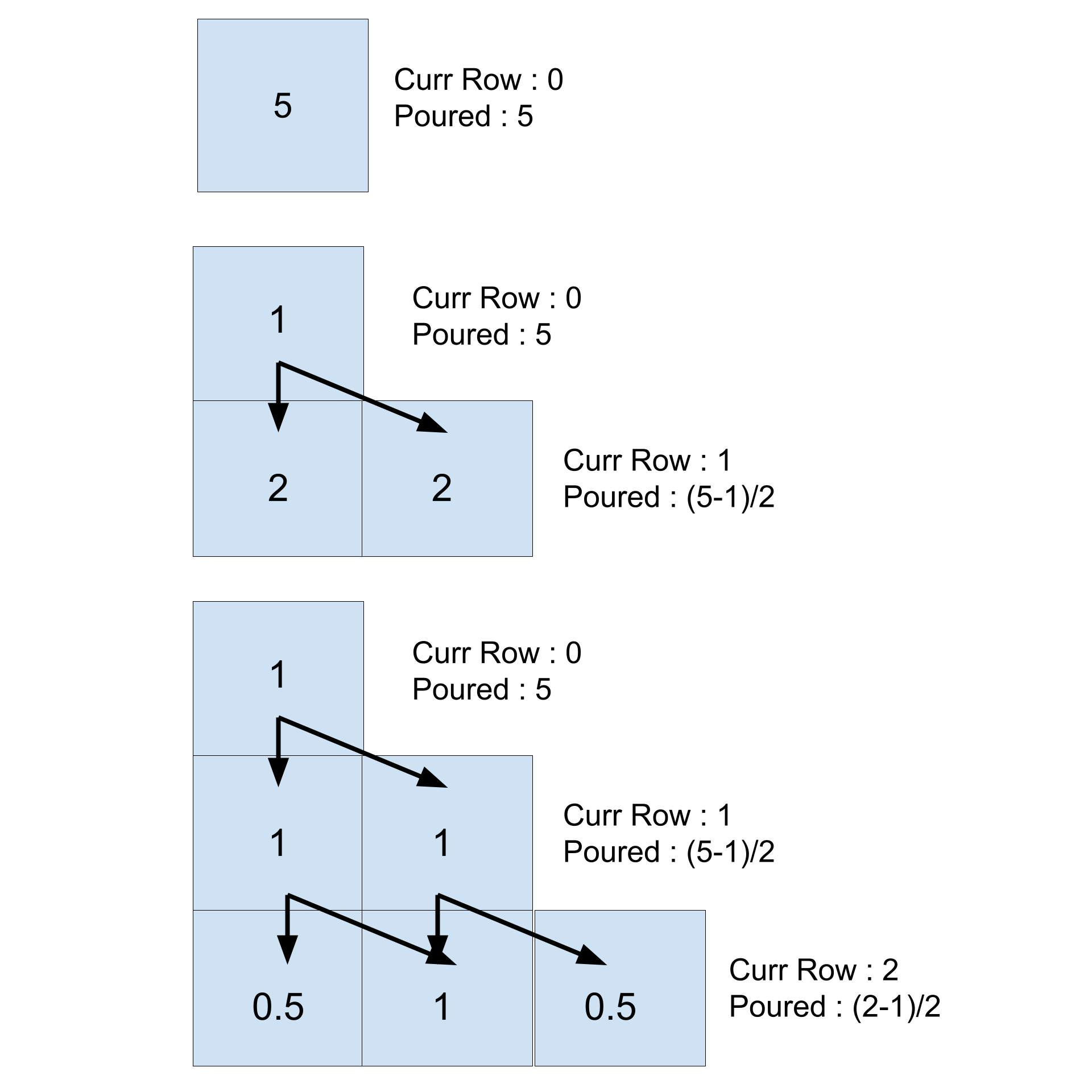
• In Step 1 the whole champagne is being poured into the first row (1 glass in the first row)
• Now, whatever is being overflowed from this glass, goes to the 2 glasses just below this glass, equally, in the second row. Equally means, half of the champagne being overflowed goes to the first glass and half of that goes to the second glass.
• Now, in the second row, from each glass whatever is being overflowed goes to the 2 glasses just below each glass, equally, in the third row. So from each glass in the second row, half of what is being overflowed goes to the left glass below it and half goes to the right glass.
• And this goes on…

Now: there will be i+1 glasses in an ith row (0-indexed) and i+2 glasses in the i+1th row (i.e if we are at row i then the next row will have i+2 glasses).

Champagne Tower LeetCode Solution

Code

C++ Code For Champagne Tower

class Solution {
public:
    double champagneTower(int poured, int query_row, int query_glass) {
        vector<double> currRow(1, poured);
    
        for(int i=0; i<=query_row; i++){ //we need to make the dp matrix only till query row. No need to do after that
            vector<double> nextRow(i+2, 0); //If we are at row 0, row 1 will have 2 glasses. So next row will have currRow number + 2 number of glasses.
            for(int j=0; j<=i; j++){ //each row will have currRow number + 1 number of glasses.
                if(currRow[j]>=1){ //if the champagne from the current glass is being overflowed.
                    nextRow[j] += (currRow[j]-1)/2.0; //fill the left glass with the overflowing champagne
                    nextRow[j+1] += (currRow[j]-1)/2.0; //fill the right glass with the overflowing champagne
                    currRow[j] = 1; //current glass will store only 1 cup of champagne
                }
            }
            if(i!=query_row) currRow = nextRow; //change the currRow for the next iteration. But if we have already reached the query_row, then the next iteration will not even take place, so the currRow is the query_row itself. So don't change as we need the currRow only.
        }
        return currRow[query_glass];
    }
};

Java Code for Champagne Tower

class Solution {
public double champagneTower(int poured, int queryRow, int queryGlass) {
  if (poured == 0)
    return 0;
  var prevRow = new ArrayList<>(List.of((double) poured));

  while (queryRow-- > 0) {
    var currentRow = new ArrayList<Double>();
    var champagneInEnds = Math.max(0, (prevRow.get(0) - 1) / 2);  // min champagne can be 0
    currentRow.add(champagneInEnds); // first glass

    for (var i = 1; i < prevRow.size(); i++)
      currentRow.add(Math.max(0, (prevRow.get(i - 1) - 1) / 2) + // flow from top-left glass
               Math.max(0, (prevRow.get(i) - 1) / 2));     // flow from top-right glass

    currentRow.add(champagneInEnds); // last glass
    prevRow = currentRow;
  }
  return Math.min(1, prevRow.get(queryGlass)); // max champagne can be 1
}
}

Python Code for Champagne Tower

class Solution:
    def champagneTower(self, poured, query_row, query_glass):
        res = [poured] + [0] * query_row
        for row in range(1, query_row + 1):
            for i in range(row, -1, -1):
                res[i] = max(res[i] - 1, 0) / 2.0 + max(res[i - 1] - 1, 0) / 2.0
        return min(res[query_glass], 1)

Complexity Analysis for Champagne Tower LeetCode Solution

Time: O(n^2) where n is the number of rows

Space: O(r) where r is the maximum size row possible.

Reference: https://en.wikipedia.org/wiki/Dynamic_programming

 

Translate »