Clone Graph LeetCode Solution

Problem Statement

Clone Graph LeetCode Solution – We are given a reference of a node in a connected undirected graph and are asked to return a deep copy of the graph. A deep copy is basically a clone where no node present in the deep copy should have the reference to any original graph node.

Examples & Explanations

Example 1:

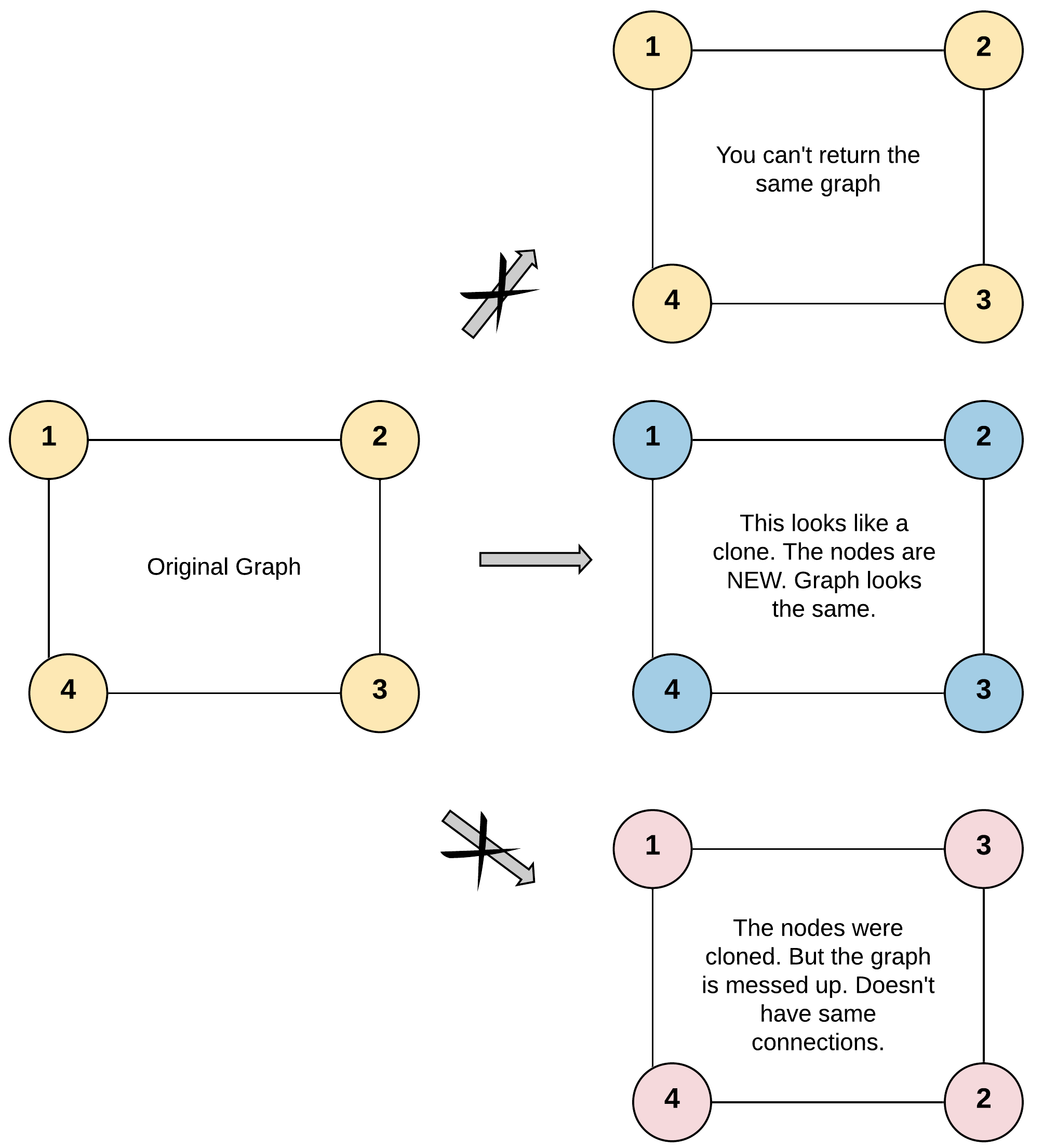
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

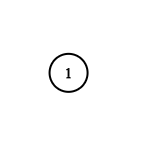
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Approach

The idea is to create an empty undirected graph. We then run DFS on the original graph. If we encounter a node that is not present in the clone, we create a new node having the same value and add it to the clone. If it is already present then simply link the required edge. Here, we have used a hashmap “vis” of type linked list, where the key will be the node referenced in the original graph and the value will be the cloned node of the original node.

Code

C++ code for Clone Graph

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
    map<Node*, Node*> vis;
    Node* dfs(Node* node) {
        // if the node is NULL simply return NULL
        if(node == NULL) {
            return node;
        }
        // if the node is already present in the vis, then return reference of that node
        if(vis.find(node) != vis.end()) return vis[node];
        
        // make a new node and store the value of original node
        Node* newNode = new Node(node->val);
        vis[node] = newNode;
        
        // traverse through neighbors of node and push back dfs of each neighbor
        for(Node* edges: node->neighbors) {
            newNode->neighbors.push_back(dfs(edges));
        }
        return newNode;
    }
public:
    Node* cloneGraph(Node* node) {
        Node* clone = dfs(node);
        return clone;
    }
};

Java code for Clone Graph

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    HashMap<Node,Node> vis = new HashMap<Node,Node>();
    public Node dfs(Node node) {
        // if the node is NULL simply return NULL
        if(node == null) {
            return node;
        }
        // if the node is already present in the vis, then return reference of that node
        if(vis.containsKey(node)) return vis.get(node);
        
        // make a new node and store the value of original node
        Node newNode = new Node(node.val);
        vis.put(node, newNode);
        
        // traverse through neighbors of node and push back dfs of each neighbor
        for(Node edges: node.neighbors) {
            newNode.neighbors.add(dfs(edges));
        }
        return newNode;
    }
    public Node cloneGraph(Node node) {
        Node clone=dfs(node);
        return clone;
    }
}

Complexity Analysis for Clone Graph LeetCode Solution

• Time Complexity: O(N+M), where N is a number of nodes (vertices) and M is a number of edges.
  • DFS takes O(N+M) time
• Space Complexity: O(N).
  • The space required by hash map “vis” will also be occupied by the recursion stack in running DFS on the given graph.
  • Let H be the height of the given graph, recursion stack will take O(H) space
  • Total, this will occupy O(N) space