Contiguous Array LeetCode Solution

Table of Contents

Problem Statement

Contiguous Array LeetCode Solution – Given a binary array nums, return the maximum length of a contiguous subarray with an equal number of 0 and 1.

Input: nums = [0,1]
Output: 2
Explanation: [0, 1] is the longest contiguous subarray with an equal number of 0 and 1.

Explanation

Now what we will do is, convert all the “0” to “-1” in the example, so we get something like:- [1, -1, -1, 1, -1, 1, 1]. If you see this, the problem is somewhat like returning the longest subarray length whose sum is “ZERO”
Because equal no. of 1’s & 0’s, so we had replaced 0 with -1. So, that means the same as well there will be equal no. of 1 & -1.

That’s the thing if in any subarray there is an equal no. of 1 & -1 their sum will be 0. We have to return that subarray length, whose sum is 0. And we have to find the longest subarray.

Let’s just see how we will solve this problem using HashMap.
We will use the help of cumulative sum, which means what is the sum from the 0th index to the 6th index.

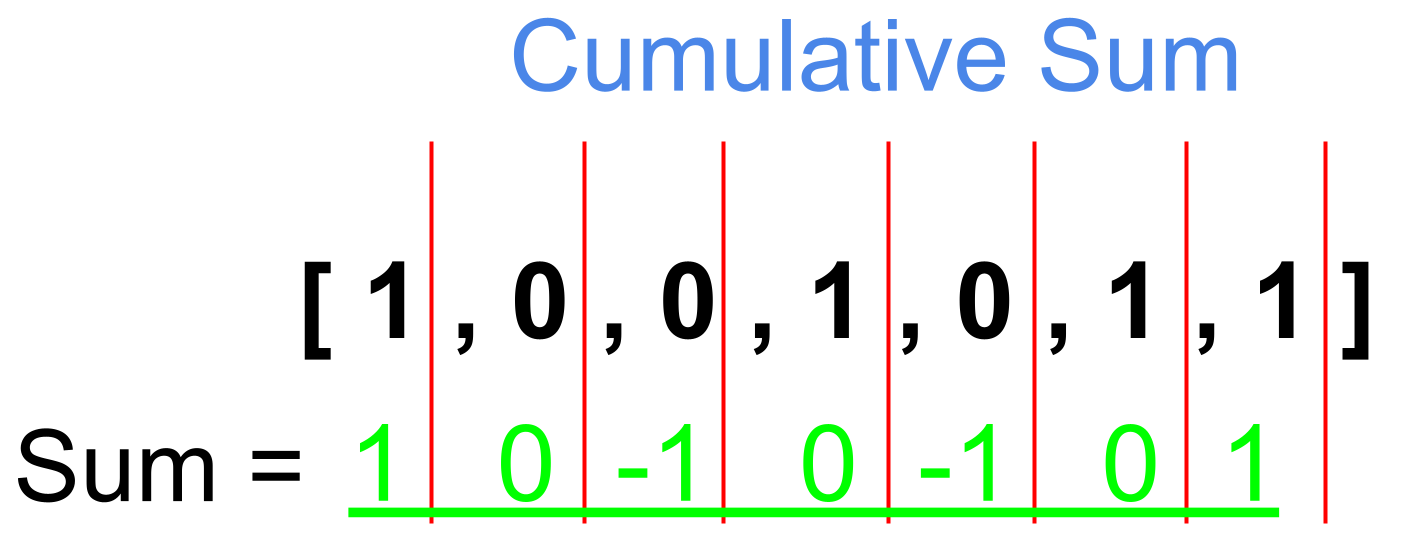
Using this cumulative sum, we will solve this problem in O(N).
In our hashMap, we will have key & value.

Initially let’s assume our gain is 0 & we are standing at an index of -1
We move forward and get a gain of 1. And in our hashmap for reference, we put key 0 -> -1 value. Why this, because initially we are at no-where & our gain is 0 & our final answer is 0 at index -1. Just hold on you will understand
At index 0 we get 1. And if we look in our HashMap, do we have key-value pair for 1? No, then we will create key 1 -> 0 value pair in hashmap. Our cumulative sum is 0 + 1 = 1
Now moving to index 1 we get a gain of -1 & loss of 1. Now our gain becomes 0 because Our cumulative sum is 1 + (-1) = 0 so what does it represent is in the Journey from -1th index to 1st index, we found a subarray i.e. [1, 0]. The subarray has equal no. of 0s & 1s. Now to calculate its length we started the journey from index -1 to index 1. Thus, 1 - (-1) = 2.
So, to trace this 2 we put our initial key 0 & value -1. Now hope you got an idea a bit, anyways. We will update it’s current & final-ans with 2
Now moving further & at index 2 we got a gain of -1 as Our cumulative sum is 0 + (-1) = -1 And if we look at hashmap -1 is not present we will make key-value pair of -1 -> 2.
Now moving further & at index 3 we get 1 & our gain becomes 0 as Our cumulative sum is 1 + (-1) = 0. And if we look at the hashmap 0 is present with a value of -1. Now to calculate its length we started the journey from index 2 to index 3. Thus, 3 - (-1) = 4, then update our current & final-ans with 4 And Till now we have found a subarray of size 4
Now moving further & at index 4 we got a gain of -1 as Our cumulative sum is 0 + (-1) = -1. And if we look at the hashmap -1 is present at the key-value pair of -1 -> 2. We got one more subarray in the Journey from the 3rd index to the 4th index. But, if we calculate its length, it will be 4 - (+2) = 2 & update our current with 2 and compare with final-ans i.e. 4 which is less, we will not consider it.
Now moving further & at index 5 we get 1 & our gain becomes 0 as Our cumulative sum is 1 + (-1) = 0. We got one more subarray in the Journey from the 4th index to the 5th index. calculate its length, it will be 5 - (-1) = 6, then update our current & final-ans with 6.
Finally moving at index 6th, we get 1 & our gain becomes 1 as Our cumulative sum is 0 + 1 = 1 . And if we look at the hashmap 1 is present at the key-value pair of 1 -> 0. We got one more subarray in the Journey from the 5th index to the 6th index. As we calculate its length, it will be 6 - (0) = 6 & compare with current & final-ans i.e. 6 which is equal to it.
In the end, we get 2 big subarrays having equal no. of 1s & 0s
[1,0,0,1,0,1]
[0,0,1,0,1,1]

Code

Java Code for Contiguous Subarray

class Solution {
    public int findMaxLength(int[] nums) {
        if (nums == null || nums.length == 0) { // Base Case
            return 0;
        }
        // Converting all 0 to -1
        for(int i = 0; i < nums.length; i++){
            if(nums[i] == 0) nums[i] = -1;
        }
        int sum = 0; // current
        int max = 0; // final-ans
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, -1); // put reference in the starting of 0 & -1, as i have tell you in the starting  
        for(int i = 0; i < nums.length; i++){
            sum += nums[i]; // cumulative sum
            if(map.containsKey(sum)){ // if cumulative sum key :- 0, -1, 1 already present
                int last = map.get(sum); // we get it's value
                max = Math.max(max, i - last); // and update max
            }
            else{ // if it's not present then create it's key-value pair
                map.put(sum, i);
            }
        }
        return max; // finally return it
    }
}

C++ Code for Contiguous Subarray

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        unordered_map<int,int> mp; //map of <gain,index> form
        mp[0]=-1; //add starting index with default gain of 0 at -1
        //change all zeros to -1
        for(int i=0;i<nums.size();i++){
            nums[i]==0?nums[i]=-1:nums[i]=1;
        }
        int sum=0,res=0;
        for(int i=0;i<nums.size();i++){
            //cumulative sum
            sum+=nums[i];
            
            //check if value already exists in the map
            if(mp.find(sum)!=mp.end()){
                //finding the length of possible subarray and comparing with the max result
                res=max(res,i-mp[sum]);
            }
            else{
                //adding value to our map
                mp[sum]=i;
            }
        }
        return res;
    }
};

Python Code for Contiguous Subarray

class Solution(object):
    def findMaxLength(self, nums):
        count = 0
        max_length=0
        table = {0: 0}
        for index, num in enumerate(nums, 1):
            if num == 0:
                count -= 1
            else:
                count += 1
            
            if count in table:
                max_length = max(max_length, index - table[count])
            else:
                table[count] = index
        
        return max_length