Design Skiplist LeetCode Solution

Table of Contents

Problem Statement

Design Skiplist LeetCode Solution – Design a Skiplist without using any built-in libraries.

A skip list is a data structure that takes O(log(n)) time to add, erase and search. Compared with the tree and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skip lists is just simple linked lists.

For example, we have a Skiplist containing [30,40,50,60,70,90] and we want to add 80 and 45 into it. The skiplist works this way:

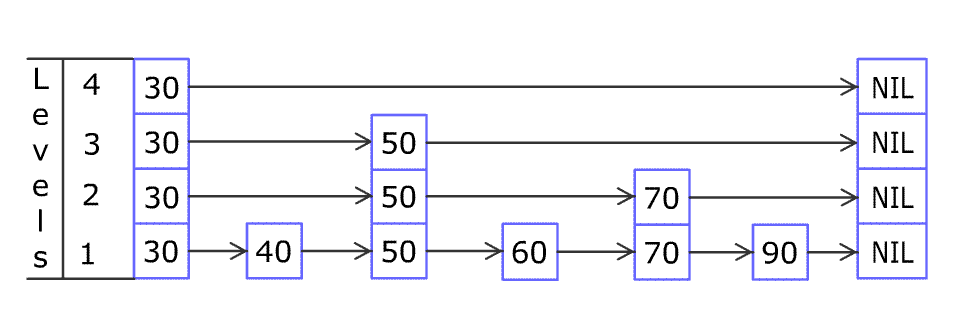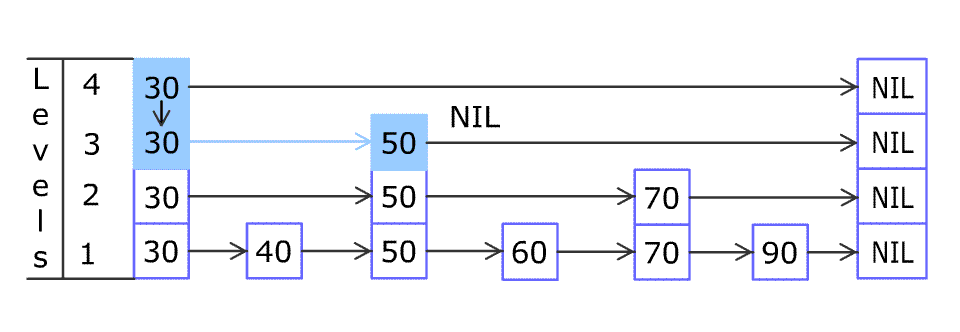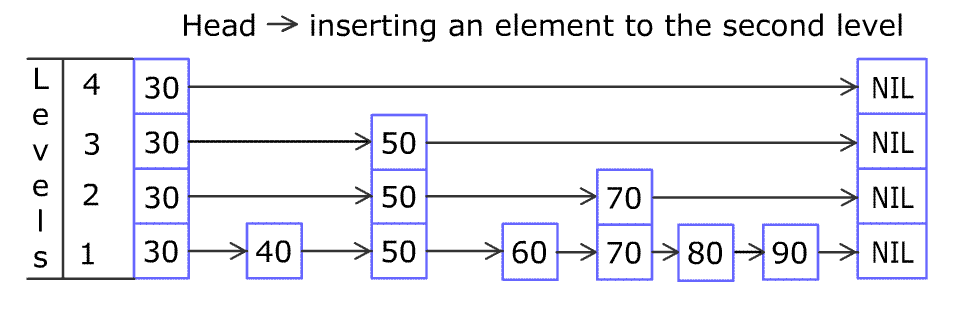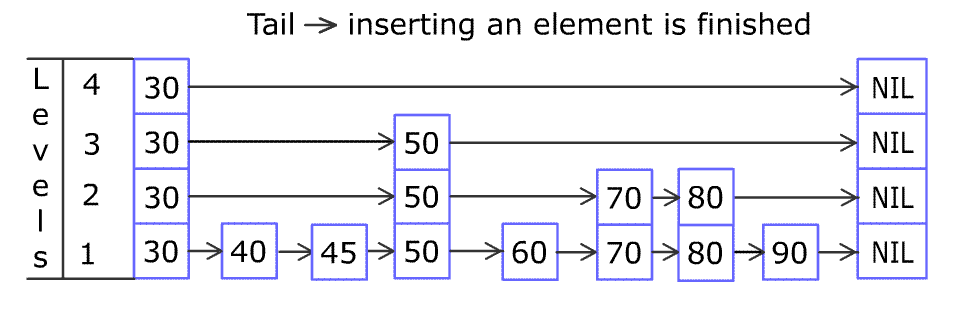
You can see there are many layers in the skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than O(n). It can be proven that the average time complexity for each operation is O(log(n)) and space complexity is O(n).

See more about Skiplist: https://en.wikipedia.org/wiki/Skip_list

Implement the Skiplist class:

Skiplist() Initializes the object of the skiplist.
bool search(int target) Returns true if the integer target exists in the Skiplist or false otherwise.
void add(int num) Inserts the value num into the SkipList.
bool erase(int num) Removes the value num from the Skiplist and returns true. If num does not exist in the Skiplist, do nothing and return false. If there exist multiple num values, removing any one of them is fine.

Note that duplicates may exist in the Skiplist, your code needs to handle this situation.

Input
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
Output
[null, null, null, null, false, null, true, false, true, false]

Explanation
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0);  // return False, 0 is not in skiplist.
skiplist.erase(1);  // return True
skiplist.search(1); // return False, 1 has already been erased.

Explanation

Skip lists are an alternative to balanced trees or self-adjusting trees and they are definitely easier to implement than RB or AVL trees. They are balanced by consulting a random number generator. In this code, I am using rand().

This code can be improved if we knew n (number of elements to be added to the skiplist) which is not provided upfront. With that information, it would be easy to find a max level – say for 32K elements, we could have a max level of 15 (2^15 = 32K). The intermediate columns we construct randomly could then be limited to this max level. Also, in this code, we don’t restrict raising columns – they can be raised while inserting an element at level 0. So, one improvement to make would be not to raise a column randomly and do it for every m node at level 0.

Level 5:

Level 4:------->3---->NULL

Level 3:------->3---->NULL

Level 2:------->3---->NULL

Level 1:---->2->3->4->NULL

Level 0:->1->2->3->4->NULL

Code

C++ Code for Design Skiplist

class Skiplist {
private:
    struct sle { int val; sle *down, *next; };
    vector<sle *> head;
    int level = 0;
    
    /* Debugging - visualize how the skip list looks */
    void visual(void) {
        for (int i = level; i >= 0; i--) {
            sle *p = head[i];
            cout << "Level " << i << ":";
            while(p) { if (p->val >= 0) cout << p->val << " "; p = p->next; }
            cout << endl;
        }
    }

public:
    Skiplist() {
        return;
    }

    bool search(int target) {
        sle *p = head[level];   /* start from the highest level */
        while (p) {
            if (p->val == target) return 1; /* found */
            /* If the next node is higher than target, descend down the column to lower level */
            if (p->next == NULL || (p->next && p->next->val > target)) { p = p->down; continue; }
            p = p->next;
        }
        return 0;
    }
    
    void add(int num) {
        int l = 0 /* start at level 0 */, once = 0;     /* at least one loop is required */ 
        sle *ln = NULL;                                 /* last lower node */
        while (!once++ || (rand() % 2)) {               /* at least once OR as long as coin flip is 1 */
            sle *n = new sle; n->val = num, n->down = ln, n->next = NULL;   /* allocate a skip list entry node, 
                                                        /* with down pointing to node in this column at level below */
            
            /* First time init of skip list - add a sentinel node and the new node */
            if (head.size() == 0) {                     
                sle *sn/*sentinel node */ = new sle; sn->val = INT_MIN, sn->next = n, sn->down = NULL;
                head.push_back(sn); return; 
            }
            
            /* Insert node at level l */
            sle *p = head[l], *last = NULL;
            while (p) { if (p->val >= num) { last->next = n; n->next = p; break; } last = p; p = p->next; }
            if (!p) last->next = n;

            /* We need one more level - promote the sentinel node to new level */
            if (++l > level) {
                sle *sn/*sentinel node */ = new sle; sn->val = INT_MIN; sn->next = NULL; sn->down = head[level];
                head.push_back(sn); 
                level++;
            }
            
            /* Record node at this level to be used for down field of node at upper level */
            ln = n;
        }
    }
    
    bool erase(int num) {
        sle *p = head[level]; /* start at highest level */ bool del = 0;
        while (p) {
            /* If next node is end of list or is greater than num, descend down the column */
            if (p->next == NULL || p->next->val > num) { p = p->down; continue; }
            
            /* if found, delete it at this level and continue on to next lower level */
            if (p->next && p->next->val == num) {   
                p->next = p->next->next; 
                del = 1; 
                p = p->down; continue; 
            }
            p = p->next;
        }
        return del;
    }
};

Java Code for Design Skiplist

class Skiplist {
    class Node {
        int val;
        Node next, down;
        public Node(int val, Node next, Node down) {
            this.val = val;
            this.next = next;
            this.down = down;
        }
    }
    Node head = new Node(-1, null, null);
    Random rand = new Random();
    public Skiplist() {
        
    }
    
    public boolean search(int target) {
        Node cur = head;
        while (cur != null) {
            while (cur.next != null && cur.next.val < target) {
                cur = cur.next;
            }
            if (cur.next != null && cur.next.val == target) return true;
            cur = cur.down;
        }
        return false;
    }
    
    public void add(int num) {
        Stack<Node> stack = new Stack<>();
        Node cur = head;
        while (cur != null) {
            while (cur.next != null && cur.next.val < num) {
                cur = cur.next;
            }
            stack.push(cur);
            cur = cur.down;
        }
        boolean insert = true;
        Node down = null;
        while (insert && !stack.isEmpty()) {
            cur = stack.pop();
            cur.next = new Node(num, cur.next, down);
            down = cur.next;
            insert = rand.nextDouble() < 0.5;
        }
        if (insert) head = new Node(-1, null, head);
    }
    
    public boolean erase(int num) {
        Node cur = head;
        boolean found = false;
        while (cur != null) {
            while (cur.next != null && cur.next.val < num) {
                cur = cur.next;
            }
            if (cur.next != null && cur.next.val == num) {
                found = true;
                cur.next = cur.next.next;
            }
            cur = cur.down;
        }
        return found;
    }
}

Design Skiplist LeetCode Solution

Problem Statement

Explanation

Code

C++ Code for Design Skiplist

Java Code for Design Skiplist

Complexity Analysis for Design Skiplist LeetCode Solution

Time Complexity

Space Complexity