Distance Between Bus Stops Leetcode Solution

Difficulty Level Easy
Frequently asked in Google
algorithms Array coding Interview interviewprep LeetCode LeetCodeSolutionsViews 2998

The problem Distance Between Bus Stops Leetcode Solution provides us an array of integers describing the distance between the adjacent cities. The cities are given in a circular order. So, the last city is followed by the first city. Now, we are required to find out the minimum distance between the two given cities. So, before moving onto the solution. Let’s see a few examples.

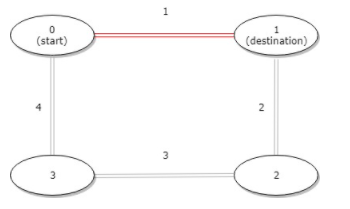
Distance Between Bus Stops Leetcode Solution

distance = [1,2,3,4], start = 0, destination = 1
1

Explanation: The cities arranged in circular order are shown in the image above. Here, in the example, we are provided city 0 as the starting city and city 1 as the destination. So, there are two ways possible to start from city 0 and reach city1. Either we can simply go from city 0 to 1. Or we can follow the path from 0 to 3, 3 to 2, 2 to 1. Now, we will calculate the distance to be traveled from both ways and return the minimum distance. The first path 0 to 1, requires us to travel distance = 1, while the other path requires us to travel distance = 9. Thus the minimum distance is 1 unit.

distance = [1,2,3,4], start = 0, destination = 2
3

Explanation: Just as we did in the above example, we calculate the distance in both directions, and return the minimum. Since the two paths are of length 3 and 7. We pick the minimum of the two that is 3.

Approach for Distance Between Bus Stops Leetcode Solution

The problem Distance Between Bus Stops Leetcode Solution asked to find the minimum distance required to travel if starting city and destination city are given to us. The problem is simple because there can be only two ways to reach the destination. One is if we start in the direction of moving forward and the other moving backward and reaching the destination. We can find the distance for one of the journeys, and the other can be easily calculated by subtracting this distance from the total.

Consider, we need to go from city 2 to 5, where a total number of cities is 10. Then we either go from 2 to 5. Or go from 5 to 10, then 10 to 1, and then 1 to 2. The result of the union of both paths is the entire circuit. Thus, we can subtract the distance to get the distance for the other journey.

Code

C++ code for Distance Between Bus Stops Leetcode Solution

#include<bits/stdc++.h>
using namespace std;

int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
    if(start>destination)swap(start, destination);
    int total = 0, first_path = 0;
    for(int i=0;i<distance.size();i++){
        if(i>=start && i<destination)
        first_path += distance[i];
        total += distance[i];
    }
    return min(total - first_path, first_path);
}

int main(){
    vector<int> distance = {1, 2, 3, 4};
    cout<<distanceBetweenBusStops(distance, 0, 1);
}

1

Java code for Distance Between Bus Stops Leetcode Solution

import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
  public static int distanceBetweenBusStops(int[] distance, int start, int destination) {
        if(start>destination){
            int t = start;
            start = destination;
            destination = t;
        }
        int total = 0, first_path = 0;
        for(int i=0;i<distance.length;i++){
            if(i>=start && i<destination)
            first_path += distance[i];
            total += distance[i];
        }
        return Math.min(total - first_path, first_path);
    }
    
  public static void main (String[] args) throws java.lang.Exception
  {
    int[] distance = {1, 2, 3, 4};
    System.out.println(distanceBetweenBusStops(distance, 0, 1));
  }
}
1

Complexity Analysis

Time Complexity

O(N), where N is the number of cities. Since we had to travel through all the cities. The time complexity is linear.

Space Complexity

O(1), since we used only a single variable. The space complexity is constant.

Translate »