Find First and Last Position of Element in Sorted Array Leetcode Solution

Difficulty Level Medium
Frequently asked in Amazon Bloomberg ByteDance Facebook Google Microsoft Oracle Uber
algorithms Array coding Interview interviewprep LeetCode LeetCodeSolutionsViews 5771

Problem statement

In this article titled “Find First and Last Position of Element in Sorted Array Leetcode Solution,” we will discuss the solution to a leetcode problem. In the given problem we are given an array. We are also given a target element. Elements in the array are sequenced in increasing order.

We need to find the first and last position of the target element in the sorted array.

If the target element is not present then return [-1,-1].

Example

array: [1,2,5,5,5,9] , target=5
[2,4]

Explanation:

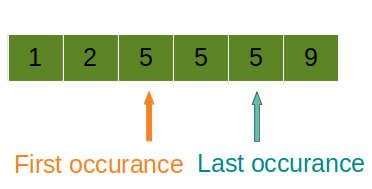
Find First and Last Position of Element in Sorted Array Leetcode Solution

As in the given sorted array, 5 appears for the first time at index number 2 and last time at index number 4.

Approach

The naive approach to solve this problem is to scan the whole array and return the index when we encounter the target for the first time and last time. The time complexity for this algorithm is O(n) as in the worst case we may need to traverse the complete array.

As the elements are sorted in increasing order, we can take advantage of it. In spite of doing a linear search, we will use a Binary search to find the first and last occurrences of the target element. This binary search code will be a little bit different from the normal binary search code where we check if the element is present in the sorted array or not.

These are the small changes in normal binary search code:

  1. The program will not terminate immediately after finding the target element. We will run the loop till start=end.
  2. Another change is at the point where arr[mid]==target.
    1. For the first occurrence end=mid-1.
    2. And for the last occurrence start=mid+1.

Code Find First and Last Position of Element in Sorted Array Leetcode Solution

C++ code

#include <bits/stdc++.h> 
using namespace std; 
    int findFirst(vector<int>& nums, int target)
    {
         int ans = -1;
    int s = 0;
    int e = nums.size() - 1;
    while(s <= e){
        int mid =s+ (e-s) / 2;
        if (nums[mid] < target) 
            s = mid + 1;
        else if (nums[mid] > target) 
            e = mid - 1;
        else  {
            ans = mid;
            e = mid - 1;
        }
    }
    return ans;
    }
     int findLast(vector<int>& nums, int target)
    {
          int ans = -1;
    int s = 0;
    int e = nums.size() - 1;
    while(s <= e){
        int mid =s+ (e-s) / 2;
        if (nums[mid] < target) 
            s = mid + 1;
        else if (nums[mid] > target) 
            e = mid - 1;
        else  {
            ans = mid;
            s = mid + 1;
        }
    }
    return ans;
    }
    vector<int> find(vector<int>& nums, int target) {
        vector<int>result(2);
         result[0] = findFirst(nums, target);
         result[1] = findLast(nums, target);
         return result;
    }

int main() 
{ 
 vector<int> arr = {1,2,5,5,5,9}; 
int target=5;
vector<int> ans(2);
ans=  find(arr,target);
for(int i=0;i<2;i++)
 cout<<ans[i]<<" "; 
 return 0;
}
[2,4]

Java code

import java.util.Arrays; 
public class Tutorialcup {
    public static int[] find(int[] nums, int target) {
    int[] result = new int[2];
    result[0] = findFirst(nums, target);
    result[1] = findLast(nums, target);
    return result;
}

private static int findFirst(int[] nums, int target){
    int ans = -1;
    int s = 0;
    int e = nums.length - 1;
    while(s <= e){
        int mid =s+ (e-s) / 2;
        if (nums[mid] < target) 
            s = mid + 1;
        else if (nums[mid] > target) 
            e = mid - 1;
        else  {
            ans = mid;
            e = mid - 1;
        }
    }
    return ans;
}
    

private static int findLast(int[] nums, int target){
       int ans = -1;
    int s = 0;
    int e = nums.length - 1;
    while(s <= e){
        int mid =s+ (e-s) / 2;
        if (nums[mid] < target) 
            s = mid + 1;
        else if (nums[mid] > target) 
            e = mid - 1;
        else  {
            ans = mid;
            s = mid + 1;
        }
    }
    return ans;
}
  public static void main(String[] args) {
    int [] arr = {1,2,5,5,5,9}; 
    int target=5;
     int[] ans = new int[2];
    ans=  find(arr,target);
    System.out.println(Arrays.toString(ans));
  }
}
[2,4]

Complexity Analysis

Time complexity

The time complexity of the above code is O(log(n))where n is the size of the array. Because we are processing at most log(n) elements during the binary search.

Space complexity

The space complexity of the above code is O(1) because we are using only a variable to store answers.

References

Translate ยป