Find Minimum in Rotated Sorted Array II LeetCode Solution

Problem Statement

Find Minimum in Rotated Sorted Array II LeetCode Solution – Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,4,4,5,6,7] might become:

• [4,5,6,7,0,1,4] if it was rotated 4 times.
• [0,1,4,4,5,6,7] if it was rotated 7 times.

Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].

Given the sorted rotated array nums that may contain duplicates, return the minimum element of this array.

You must decrease the overall operation steps as much as possible.

Example:

input : [1,2,3]

output – 1

Explanation :

The minimum element in the nums array is 1.

input : [2,2,2,0,1]

output – 0

Explaination :

The minimum element in nums array is 0. So we return 0.

Approach:

Idea

Since the array is sorted one might think of applying a binary search here, but a simple binary search will not work here as the array is rotated as well so we will have to carefully analyze the problem using an example.

Algorithm-

1. Keep two pointers low and high which points to the lowest and highest boundaries of our search space.
2. We then reduce the search space by moving either of the pointers according to various situations.
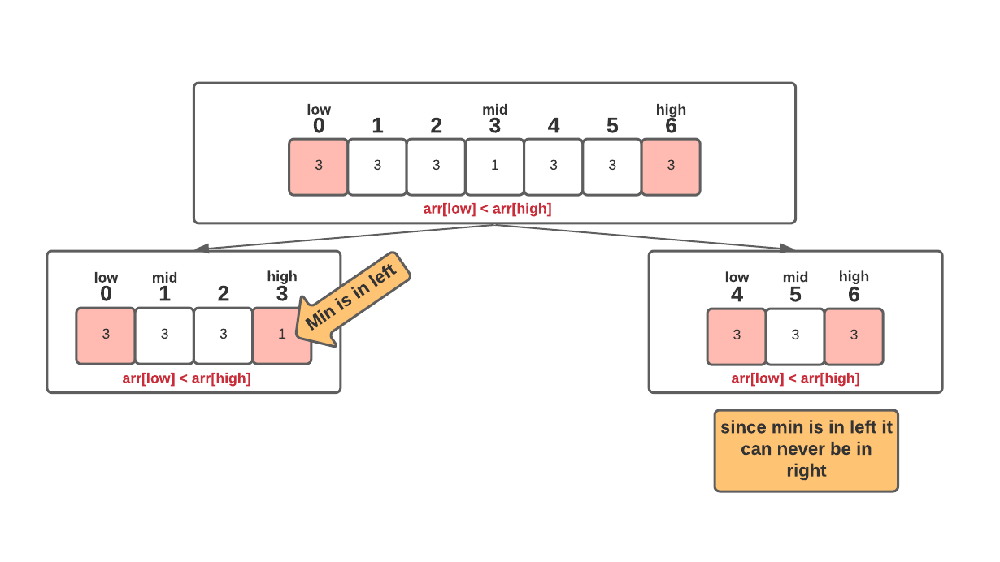
3. If the mid-value is less than the high value then, that means elements lying between mid and high are sorted in non-decreasing order so the minimum value will be at the left, so we do, high = mid.
4. If the mid-value is greater than the high value then, that means elements lying between low and mid are sorted in non-decreasing order so the minimum value will be at the right so we do low = mid+1.
5. If the mid value is equal to the high value then decrease high by 1,  high = high-1;
6. Run the above instructions till low becomes equal to high.

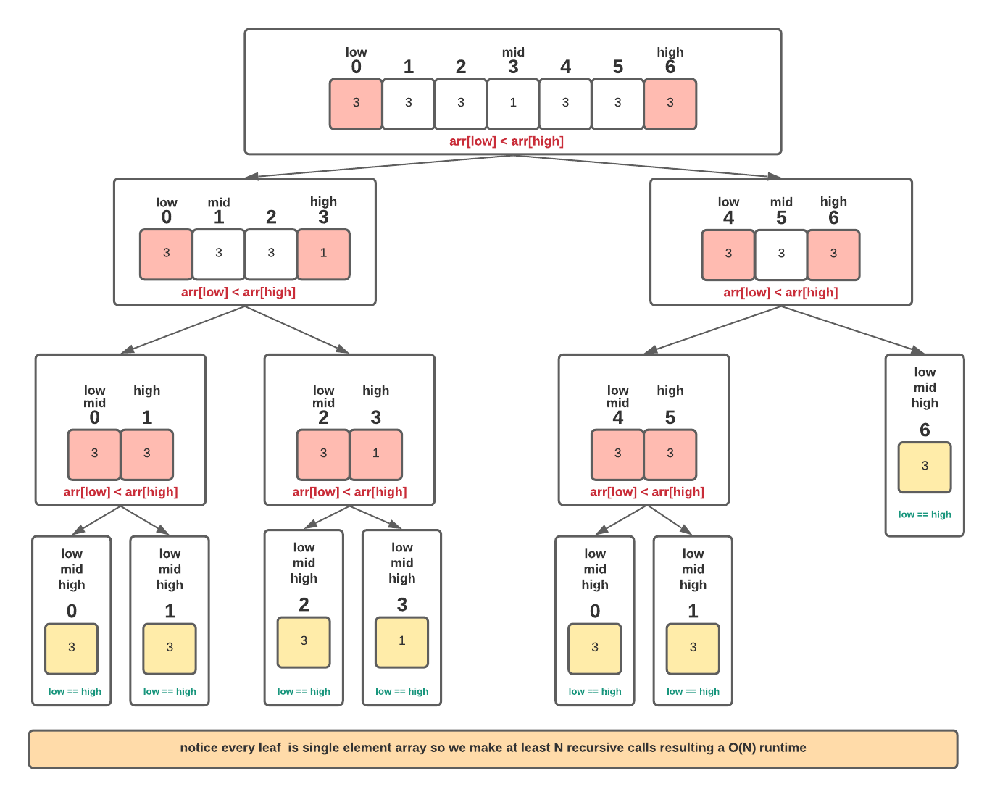
Inefficient

Efficient

Example-

nums – [2,2,2,3,4,5,5,5,0,0,1,1,1,1,2,2,2]

Step -1

low  =  0 ,  high = 16

mid = (low+high)/2 = 8

now since nums[mid] < nums[high] ,  so that means we have to move left ,

high = mid;

step – 2

low = 0, high = 8;

mid = (low+high)/2 = 4;

nums[mid] > nums[high] ,  move right,

low = mid+1;

step – 3

low = 5 , high = 8;

mid = (5+8)/2 = 6;

nums[mid] > nums[high] , move right,

low = mid+1;

step – 4

low = 7 , high = 8;

mid = (7+8)/2 = 7;

nums[mid] > nums[high] , move right,

low = mid+1;

low == high == 8, this is our minimum element’s index,

minimum element = nums[8] = 0;

Code –

C++ Code

class Solution {
public:
    int findMin(vector<int>& nums) {
        int n = nums.size();
        
        int str=0,end=n-1;
        
        while(str < end){
            int mid = str + (end-str)/2;
            
            if(nums[mid] < nums[end]){
                end = mid;
            }
            else if(nums[mid] > nums[end]){
                str = mid+1;
            }
            else{
                end-=1;
            }
        }
        return nums[str];
    }
};

Java code

class Solution {
    public int findMin(int[] nums) { 
        int low = 0;
        int high = nums.length - 1; 
        while(low < high){ 
            int mid = (low+high)/2; 
            if(nums[mid] < nums[high]){
                high = mid; 
            } 
            else if(nums[mid] > nums[high]){
                low = mid+1; 
            } 
            else{
                high -= 1; 
            } 
        } 
        return nums[low]; 
    }
}

Time and Space Complexity Analysis for Find Minimum in Rotated Sorted Array II LeetCode Solution

Time Complexity –

Since we are using a binary search algorithm and reducing the search space by half, the average time complexity is O(logn),  but in the worst case if all the elements are equal then complexity is O(n).

Space complexity –

We are not using any extra space here, Space complexity is O(1).