Find the Distance Value Between Two Arrays Leetcode Solution

Difficulty Level Easy
Frequently asked in Uber
algorithms Array coding Interview interviewprep LeetCode LeetCodeSolutionsViews 5457

The problem Find the Distance Value Between Two Arrays Leetcode Solution provides us two arrays arr1 and arr2. Along with the two arrays, we are provided with an integer n. Then the problem asks us to find the relative distance between the given two arrays. The relative distance is defined as the number of elements in the first array that does not have any element in the second array that has a minimum absolute difference less than or equal to the given integer d. So as always before diving deep into the solution, first we should take a look at a few examples.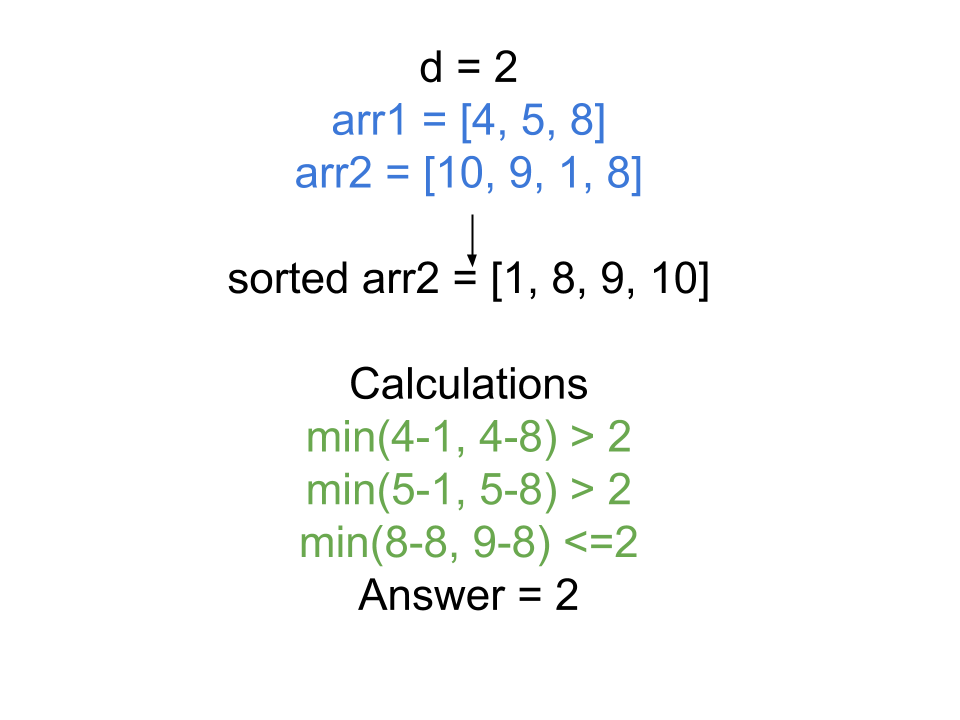Find the Distance Value Between Two Arrays Leetcode Solution

arr1 = [4,5,8], arr2 = [10,9,1,8], d = 2
2

Explanation: We will pick each element one by one from the first array to verify the output. For the first element, 4 we do not have any corresponding element in the second array that has a minimum absolute difference of 2 with it. The same goes for 5. But if we see the last element, 8, there exists an element with the same value in the second array. Thus 8, is not considered into the answer. The answer will thus become equal to 2 because of the first 2 elements of the first array.

Brute force Approach to Find the Distance Value Between Two Arrays Leetcode Solution

The brute force solution for the problem simply iterates over both the arrays picking unique pairs. Then these unique pairs are checked if the difference between them is less than the given integer ‘d’. If the difference is less than d, we flag the element. We do not count the flagged elements and the count for the remaining elements is returned as the answer. The solution is pretty straight forward but there can be a better solution.

Optimized Approach to Find the Distance Value Between Two Arrays Leetcode Solution

In the above approach, we used two nested loops. But in the end, we only needed to check if the current element in the first array has even a single element in the second array that has a difference of less than d. So, if we pick the two closest elements to the picked element from the first array. If these two closest elements do not have a minimum absolute difference of less than d, then we can say for sure that no other element can produce a better result.

So, the problem now boils down to finding the two closest elements (from the second array) to the picked element of the first array. To find these two closest elements, we sort the second array and use binary search. Using binary search we find the element that is equal or greater than the picked element. The element that is just smaller than the current element is also used to evaluate the difference.

If these differences are less than d then we flag the element and do not count it towards the answer. The rest elements are counted towards the answer and are returned at the end of the function.

Optimized code to Find the Distance Value Between Two Arrays Leetcode Solution

C++ code

#include <bits/stdc++.h>
using namespace std;

int findTheDistanceValue(vector<int>& arr1, vector<int>& arr2, int d) {
    int ans = 0;
    sort(arr2.begin(), arr2.end());
    for(int i=0;i<arr1.size();i++){
        int it = lower_bound(arr2.begin(), arr2.end(), arr1[i]) - arr2.begin();
        bool isIt = false;
        if(it<arr2.size() && abs(arr2[it] - arr1[i]) <= d)isIt = true;
        if(it != 0 && abs(arr2[it-1] - arr1[i]) <= d)isIt = true;
        if(!isIt)
            ans++;
    }
    return ans;
}

int main(){
    vector<int> arr1 = {4,5,8};
    vector<int> arr2 = {10,9,1,8};
    int d = 2;
    cout<<findTheDistanceValue(arr1, arr2, d);
}

2

Java code

import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
  private static int findTheDistanceValue(int[] arr1, int[] arr2, int d) {
        Arrays.sort(arr2);
        int ans = 0;
        for (int i= 0;i<arr1.length;i++) {
            int it = Arrays.binarySearch(arr2, 0, arr2.length, arr1[i]);
            if (it < 0) it = -(it+1);
            boolean isIt = false;
            if(it<arr2.length && Math.abs(arr2[it] - arr1[i]) <= d)isIt = true;
            if(it != 0 && Math.abs(arr2[it-1] - arr1[i]) <= d)isIt = true;
            if(!isIt)
                ans++;
        }
        return ans;
    }
    
  public static void main (String[] args) throws java.lang.Exception
  {
    int[] arr1 = {4,5,8};
      int[] arr2 = {10,9,1,8};
      int d = 2;
      System.out.print(findTheDistanceValue(arr1, arr2, d));
  }
}
2

Complexity Analysis

Time Complexity

O(max(M, N)logN), since we sort the second array and perform a binary search for each element in the first array. Here M, N is the number of elements in the first and second array respectively.

Space Complexity

O(N), space required to sort the second array.

Translate »