Flatten Binary Tree to Linked List LeetCode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Bloomberg ByteDance Facebook Goldman Sachs Google Microsoft Salesforce UberViews 956

Problem Statement:

Flatten Binary Tree to Linked List LeetCode Solution: Given the root of a binary tree, flatten the tree into a “linked list”:

  • The “linked list” should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
  • The “linked list” should be in the same order as a pre-order traversal of the binary tree.

Examples:

Example 1:

Input:

 root = [1,2,5,3,4,null,6]

Output:

 [1,null,2,null,3,null,4,null,5,null,6]

Approach:

Idea:

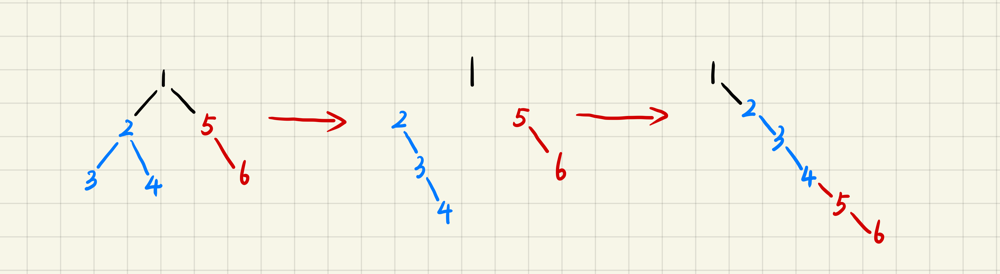
The idea is to flatten the tree in a recursive manner. We will flatten all the left and right subtrees recursively and will keep a pointer to keep track of the recently flattened subtree. the idea is, that the bottom right-most node of the current left node should point to the current right node and the current right node should point to the current left node and the current left should point to null.
if there is no current left then move to curr to the current’s right.Check out the code for a better understanding.

  1. Flatten the left subtree of the root node into a linked list;
  2. Flatten the right subtree of the root node into a linked list;
  3. Let the right subtree of step 2 be the right child of the furthest right node of the left subtree of step 1.

Obviously, that’s a recursive process.

Flatten Binary Tree to Linked List LeetCode Solution

Code:

Flatten Binary Tree to Linked List C++ Solution:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* prev = NULL;
    void helper(TreeNode* root){
        if(!root)
            return;
        helper(root->right);
        helper(root->left);
        
        root->right = prev;
        root->left = NULL;
        prev = root;
    }
    
    void flatten(TreeNode* root){
        helper(root);
    }
};

Complexity Analysis of Flatten Binary Tree to Linked List LeetCode Solution:

  • Time Complexity: The time complexity of the above code is O(n).
  • Space Complexity: The space complexity of the above code is O(n), occupied by the recursion stack.
Translate »