Greatest Sum Divisible by Three LeetCode Solution


Frequently asked in Adobe Amazon Bloomberg Facebook
DeShaw ShopeeViews 2081

Problem Statement:

Greatest Sum Divisible by Three LeetCode Solution:  Array nums of integers are given, we need to find the maximum possible sum of elements of the array such that it is divisible by three.

Example 1:

Input:

 nums = [3,6,5,1,8]

Output:

 18

Explanation:

 Pick numbers 3, 6, 1 and 8 their sum is 18 (maximum sum divisible by 3).

Example 2:

Input:

 nums = [4]

Output:

 0

Explanation:

 Since 4 is not divisible by 3, do not pick any number.

Example 3:

Input:

 nums = [1,2,3,4,4]

Output:

 12

Explanation:

 Pick numbers 1, 3, 4 and 4 their sum is 12 (maximum sum divisible by 3).

 

Constraints:

  • 1 <= nums.length <= 4 * 10^4
  • 1 <= nums[i] <= 10^4

Approach:

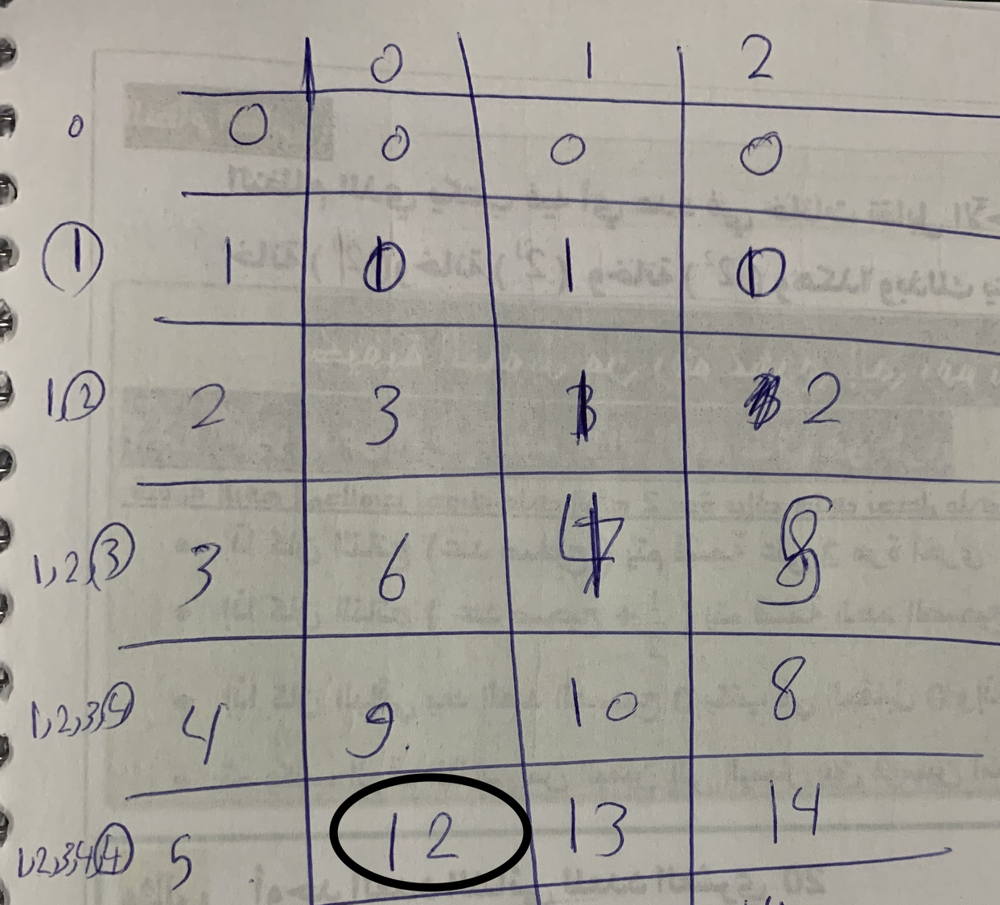
  1. This problem can be solved by using Dynamic Programming 
  2. Every number can be represented as a reminder of  3. So, num% 3 can be 0,1,2.
  3. Our dp state is represented by rec(ind, sum).
  4. rec(ind,0) = largest sum till index is divided by three.
  5. rec(ind,1)=  largest sum when divided by 3, remainder = 1.
  6. rec(ind,2)=  largest sum when divided by 3, remainder = 2.
  7. We will use include exclude principal to tackle this dp.
  8. rec(ind,sum)=max(a[ind]+rec(ind,(sum+a[ind])%3),rec(ind+1,sum)).
  9. Now discuss the base condition. If we reach the end of the array then (reminder of a sum) must be zero.
  10. We will discuss recursion with memoization.

Greatest Sum Divisible by Three LeetCode Solution

Code of Greatest Sum Divisible by Three LeetCode Solution:

C++ Code:

class Solution {
public:
    int maxSumDivThree(vector<int>& nums) {
        vector<int> dp={0,INT_MIN,INT_MIN};
    
        for(auto i: nums){
            vector<int> tmp(3);

            for(int j=0;j<3;j++){
                tmp[(j+i)%3]=max(dp[(j+i)%3],dp[j]+i);
            }

            dp=tmp;
        }

        return dp[0];
    }
};

 

Java Code:

class Solution {
    int[][] dp = new int[100005][3];
    int n;
     int rec(int ind,int sum,int[] a)
     {
         if(ind>=n)
         {
             if(sum!=0)
                 return Integer.MIN_VALUE;
             return 0;
         }
         if(dp[ind][sum]!=-1)
             return dp[ind][sum];
         int k=(sum+a[ind])%3;
         int ans1=a[ind]+rec(ind+1,k,a);
         int ans2=rec(ind+1,sum,a);
         return dp[ind][sum]=Math.max(ans1,ans2);
     }
    
    public int maxSumDivThree(int[] nums) { 
        n=nums.length;
        int i,j;
        for(i=0;i<=n;i++)
            for(j=0;j<=2;j++)
                dp[i][j]=-1;
        return rec(0,0,nums);
    }
}

Complexity Analysis for Greatest Sum Divisible by Three LeetCode Solution:

Time complexity:

Time complexity is o(n*3) or we can simply say o(n).

Space complexity:

Space complexity is o(n*3) or we can simply say o(n). We are creating a dp table to store the values.

Translate »