Insert into a Binary Search Tree Leetcode Solution

In this problem, we are given the root node of a Binary Search Tree containing integer values and an integer value of a node that we have to add in the Binary Search Tree and return its structure. After inserting the element into the BST, we have to print its Inorder Traversal.

Table of Contents

Example

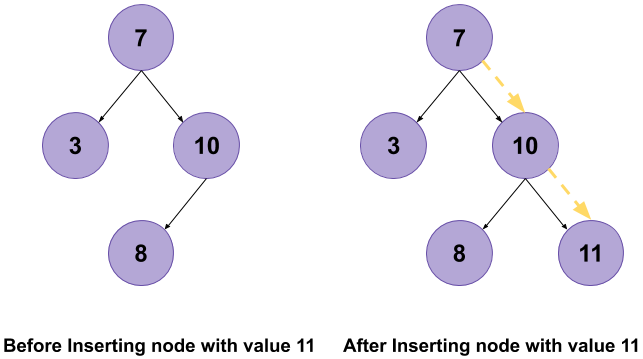
Binary Search Tree:
 
    7
 
  /     \

3         10

        /

      8
Integer Value = 11

3 7 8 10 11

Binary Search Tree:
           5

         /

       4

     /

   3
Integer Value = 2

2 3 4 5

Explanation

Approach(Recursive)

In order to decide where should any given node be inserted in our Binary Search Tree, we must set up a path from the root to the corresponding node whose left/right child will be the given node.

We can solve this recursively by passing on the task from a problem to its sub-problem. In this case, inserting a new node into a tree means to insert it to either its left subtree or right subtree. The same idea also holds for any further subtrees. We need to set up a base case. When we reach a point where the root node of any subtree is NULL, it would mean that we have reached the end of the path to insert the target node. So, we return a new node address having node value as the given value. Binary Search Trees have a significant advantage to search for any arbitrary element in O(logN) time under average cases. So, in this case, we find the position of the new node to be inserted in efficient time.

Algorithm

Create a function insertIntoBST() which returns the address of the root of BST after inserting the given node
insertIntoBST() has two parameters: root of the tree and value of the node to be inserted
The function will do the following:
- If root is NULL, return a new tree node with value same as the given value
- If the given value is greater than value of root node, then call the same problem to the right subtree and then return the root
  - root.right = insertIntoBST(root->right , value)
  - return root
- Else search in the left subtree as:
  - root.left= insertIntoBST(root.left, value)
  - return root
Print the inorder traversal of the Binary Search Tree

Implementation of Insert into a Binary Search Tree Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;
struct BSTNode
{
    int value;
    BSTNode *left , *right;
    BSTNode(int x)
    {
        value = x;
        left = NULL;
        right = NULL;
    }
};

void inorderTraversal(BSTNode* root)
{
    if(root == NULL)
        return;
    inorderTraversal(root->left);
    cout << root->value << " ";
    inorderTraversal(root->right);
    return;
}


BSTNode* insertIntoBST(BSTNode* root , int val)
{
    if(root == NULL)
        return new BSTNode(val);
    if(val > root->value)
    {
        root->right = insertIntoBST(root->right , val);
        return root;
    }
    root->left = insertIntoBST(root->left , val);
    return root;
}

int main()
{
    BSTNode* root = new BSTNode(7);
    root->left = new BSTNode(3);
    root->right = new BSTNode(10);
    root->right->left = new BSTNode(8);
    int val = 11;
    root = insertIntoBST(root , val);
    inorderTraversal(root);
    return 0;
}

Java Program

class BSTNode
{
    int value;
    BSTNode left , right;

    BSTNode(int val)
    {
        value = val;
        left = right = null;
    }
}

class insert_into_BST
{
    public static void main(String args[])
    {
        BSTNode root = new BSTNode(7);
        root.left = new BSTNode(3);
        root.right = new BSTNode(10);
        root.right.left = new BSTNode(8);
        int val = 11;
        root = insertIntoBST(root , val);
        inorderTraversal(root);
    }

    static BSTNode insertIntoBST(BSTNode root , int val)
    {
        if(root == null)
            return new BSTNode(val);
        if(val > root.value)
        {
            root.right = insertIntoBST(root.right , val);
            return root;
        }
        root.left = insertIntoBST(root.left , val);
        return root;
    }

    static void inorderTraversal(BSTNode root)
    {
        if(root == null)
            return;
        inorderTraversal(root.left);
        System.out.print(root.value + " ");
        inorderTraversal(root.right);
        return;
    }
}

3 7 8 10 11

Complexity Analysis of Insert into a Binary Search Tree Leetcode Solution

Time Complexity

O(H) = Height of BST = logN (where N = number of nodes in BST) in average cases(as we make logN recursive calls). But O(N) in the worst case when the tree is a skewed one. Because in case the tree is skewed, the search becomes a linear one.

Space complexity

O(H) in average cases. O(N) in the worst case. The case with Space Complexity is same as Time Complexity here as it depends on the number of recursive calls we make.

Approach(Iterative)

We can follow the above approach iteratively to improve on space complexity. Recursion uses stack frames which consume memory. So, in the iterative solution, we prevent the recursive call load and go down the tree on our search path until we strike a node whose either of left or right is NULL. When we have root.left/root.right= NULL, we set this node equal to a new node with value same as the given value. Note that we decide the path by comparing the values with root value in every recursion call.