Largest Submatrix With Rearrangements LeetCode Solution

Problem Statement

Largest Submatrix With Rearrangements LeetCode Solution – You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.

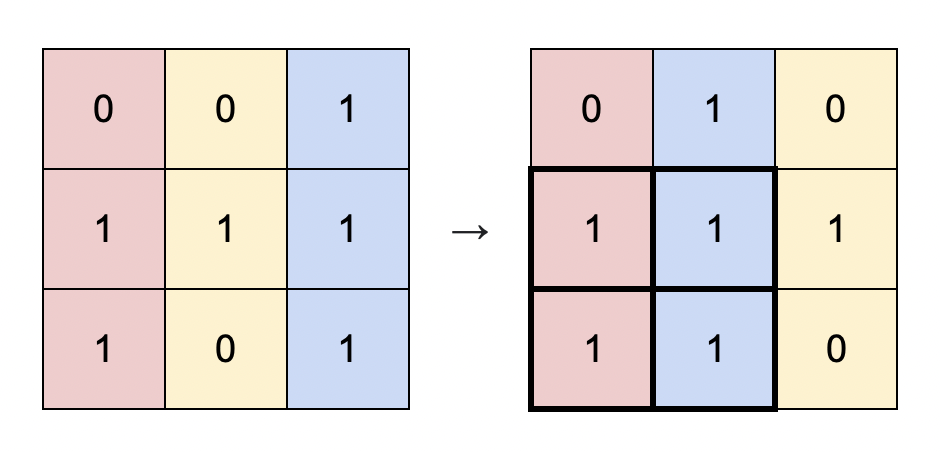
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Explanation

The question is very similar to Maximal Rectangle and Largest Rectangle in Histogram.

First, think of what we can do with a collection of histograms? What is the largest rectangle we can form?

Unlike the Largest Rectangle in Histogram, the pillar in this question can be rearranged!

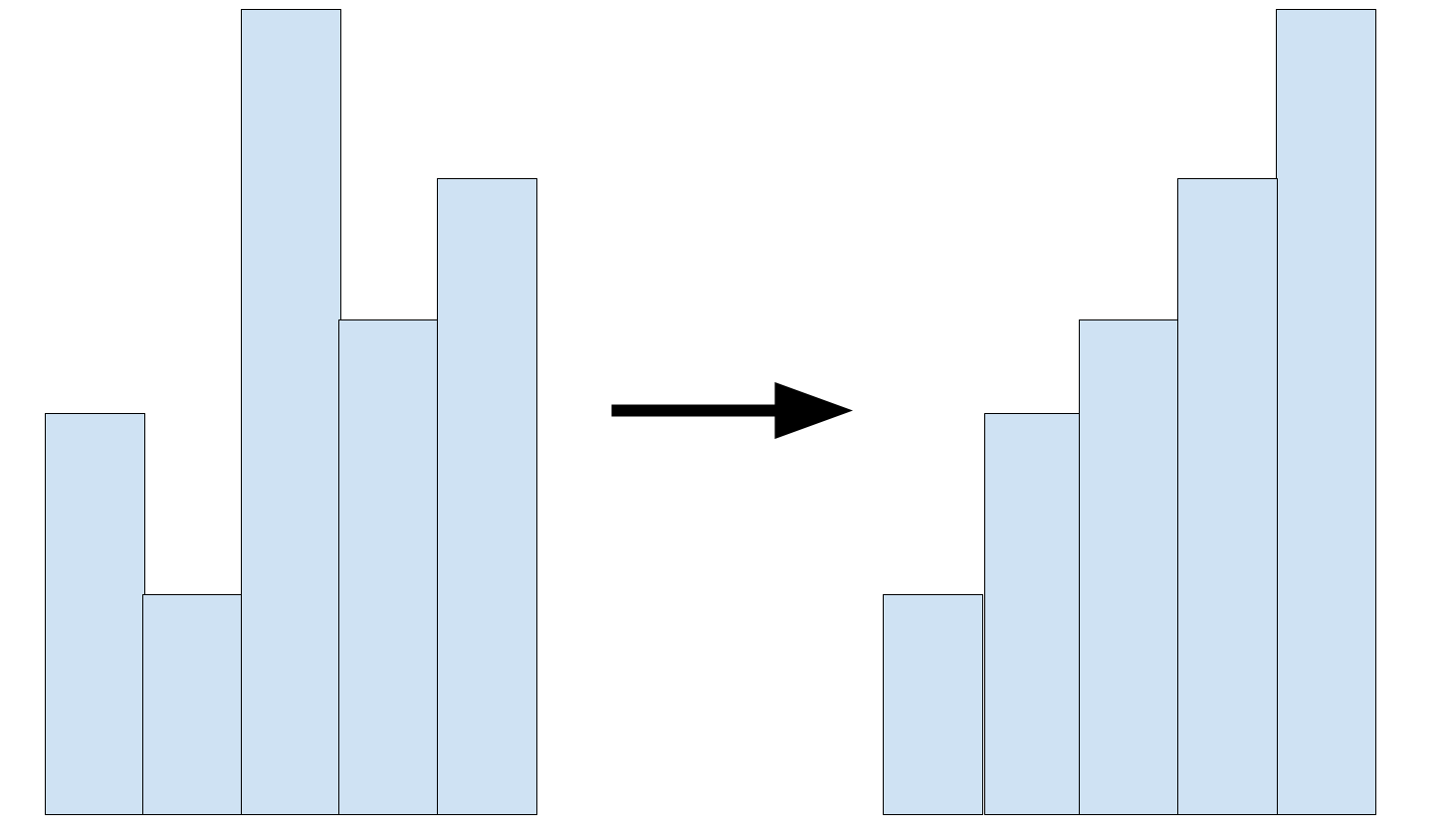
So we just iterate every pillar and calculate the maximum rectangle.

Now comes the tricky part for this question, we can view each row with its above as a collection of pillars!
And if the matrix[row][col] is 1, we add the height of pillar in the col by 1, height[row][col] = height[row - 1][col] + 1,
else if matrix[row][col] is 0, we reset the height of pillar in col as 0, height[row][col] = 0, because we can see it as the broken pillar and hence useless.

Code for Largest Submatrix With Rearrangements LeetCode Solution

 C++ Code

class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        int ans = 0;
        vector<int> height(n, 0);
    
    // view each row and its above as pillars 
        for(int i = 0; i < m; ++i){
      // calculate heights
            for(int j = 0; j < n; ++j){
                if(matrix[i][j] == 0) height[j] = 0;
                else height[j] += 1;
            }
      
      // sort pillars
            vector<int> order_height = height;
            sort(order_height.begin(), order_height.end());
      
      // iterate to get the maxium rectangle
            for(int j = 0; j < n; ++j){
                ans = max(ans, order_height[j] * (n - j));
            }
        }
        return ans;
    }
};

Java Code

class Solution {
        public int largestSubmatrix(int[][] matrix) {
        int[] len=new int[matrix[0].length];
        int res=0;
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix[i].length;j++) {
                if(matrix[i][j]==0) len[j]=0;
                else len[j]++;
            }
            int[] tmp=len.clone();
            Arrays.sort(tmp);
            for(int l=1;l<=tmp.length;l++) {
                res=Math.max(res, l*tmp[tmp.length-l]);
            }
        }
        return res;
    }
}

Python Code

class Solution:
    def largestSubmatrix(self, matrix: List[List[int]]) -> int:
        ans = 0
        for row in range(len(matrix)):
            for col in range(len(matrix[0])):
                if matrix[row][col] != 0 and row > 0:
                    matrix[row][col] += matrix[row - 1][col]

            curr = sorted(matrix[row], reverse=True) 
            for i in range(len(matrix[0])):
                ans = max(ans, curr[i] * (i + 1))
        
        return ans

Complexity Analysis for  Largest Submatrix With Rearrangements LeetCode Solution

Time: O(m*n long n)

Space: O (n)

Reference: https://en.wikipedia.org/wiki/Histogram